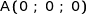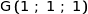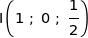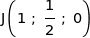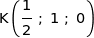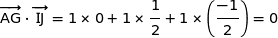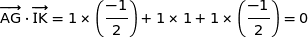Sujet et corrigé de l'exercice 3 du bac S de maths d'avril 2016 à Pondichéry
Cacher les corrigés
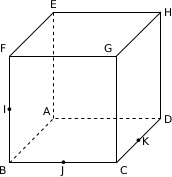
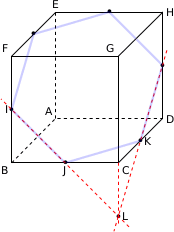
ABCDEFGH désigne un cube de côté 1.
Le point I est le milieu du segment [BF].
Le point J est le milieu du segment [BC].
Le point K est le milieu du segment [CD].
Partie A
Dans cette partie, on ne demande aucune justification
On admet que les droites (IJ) et (CG) sont sécantes en un point L.
Construire, en laissant apparents les traits de construction:
le point L ;
l'intersection
des plans (IJK) et (CDH) ;
la section du cube par le plan (IJK).
Partie B
L'espace est rapporté au repère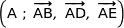 
.
1. Donner les coordonnées de A, G, I, J et K dans ce repère.
2.
a) Montrer que le vecteur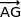 
est normal au plan (IJK).
On commence par calculer les coordonnées des vecteurs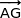 
, 
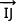et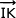 
.
Déjà les coordonnées de 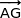sont les mêmes que celles de G, soit 
.
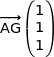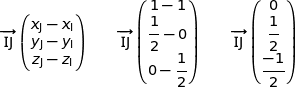
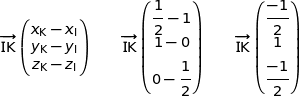
On a :
Ainsi le vecteur 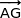est orthogonal aux vecteurs 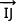et 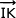qui sont deux vecteurs non colinéaires du plan (IJK). Cela entraîne que 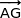est normal au plan (IJK).
b) En déduire une équation cartésienne du plan (IJK).
En utilisant le vecteur normal 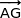nous savons qu'une équation cartésienne du plan s'écrit sous la forme :
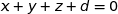
Comme le point I appartient au plan considéré, nous avons :
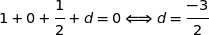
Donc une équation cartésienne de (IJK) est :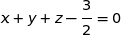 
ou encore 
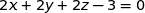si on ne veut pas de fraction.
3. On désigne par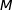 
un point du segment [AG] et 
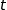le réel de l'intervalle 
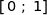tel que
.
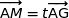a) Démontrer que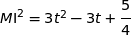 
.
Le point A étant l'origine du repère, les coordonnées de 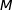sont les mêmes que celles de 
.
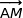Or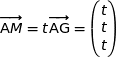 
et du coup 
.
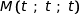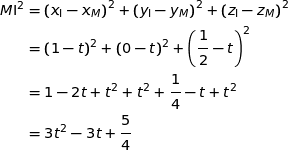
b) Démontrer que la distance 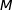I est minimale pour le point 
.
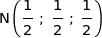La distance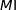 
est minimale lorsque 
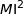est minimale, or l'expression de ce carré est un trinôme du second degré de la variable 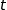de la forme 
.
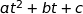Comme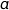 
est positif, le trinôme admet un minimum atteint pour 
.
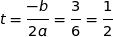Donc .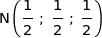
4. Démontrer que pour ce point :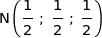
a) N appartient au plan (IJK).
Une équation cartésienne de (IJK) est .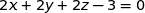
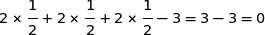
Cela montre que le point N appartient au plan (IJK).
b) La droite (IN) est perpendiculaire aux droites (AG) et (BF).
Comme I et N appartiennent au plan (IJK), la droite (IN) est incluse dans ce plan.
Le vecteur 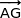est normal au plan (IJK), donc la droite (AG) est orthogonal à ce plan.
Du coup la droite (IN) du plan (IJK) est orthogonale à la droite (AG) et comme de plus N appartient également à (AG), les deux droites sont sécantes ; on peut donc dire qu'elles sont perpendiculaires.
Enfin pour terminer, nous calculons les coordonnées de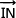 
et 
:
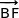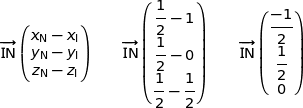
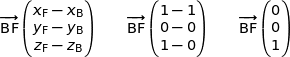
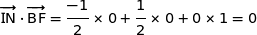
Du coup les vecteurs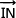
et 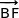sont orthogonaux ce qui entraîne que les droites (IN) et (BF) sont orthogonales. Par ailleurs le point I est sur l'arête [BF] du cube donc les droites considérées se coupent en I et par conséquent elles sont perpendiculaires.
