Sujet et corrigé de l'exercice 5 du bac S de maths d'avril 2016 à Pondichéry
Cacher les corrigés
On souhaite stériliser une boîte de conserve.
Pour cela, on la prend à la température ambiante 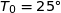 C et on la place dans un four à
température constante
C et on la place dans un four à
température constante 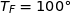 C.
C.
La stérilisation débute dès lors que la température de la boîte est supérieure à 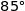 C.
C.
Les deux parties de cet exercice sont indépendantes
Partie A : Modélisation discrète
Pour  entier naturel, on note
entier naturel, on note 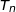 la température en degré Celsius de la boîte au bout de
la température en degré Celsius de la boîte au bout de  minutes. On a donc
minutes. On a donc 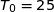 .
.
Pour  non nul, la valeur
non nul, la valeur 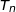 est calculée puis affichée par l'algorithme suivant :
est calculée puis affichée par l'algorithme suivant :

1. Déterminer la température de la boîte de conserve au bout de 3 minutes.
Arrondir à l'unité.
En utilisant l'algorithme la variable 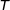 prend successivement les valeurs indiquées dans le tableau ci-dessous :
prend successivement les valeurs indiquées dans le tableau ci-dessous :
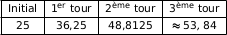
Donc arrondi à l'unité la température de la boîte de conserve au bout de 3 minutes est 54° C.
2. Démontrer que, pour tout entier naturel  , on a
, on a 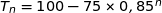 .
.
Soit 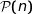 : «
: « 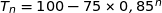 »
»
Montrons par récurrence, que 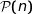 est vraie pour tout entier naturel
est vraie pour tout entier naturel  .
.
Initialisation au rang 0
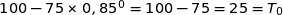
Donc 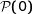 est vraie.
est vraie.
Hérédité
Supposons qu'à un rang 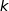 ;
; 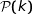 soit vraie, c'est à dire que
soit vraie, c'est à dire que 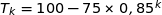 .
.
Montrons qu'alors 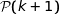 est vraie.
est vraie.
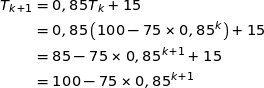
Donc 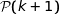 est vraie.
est vraie.
La propriété considérée est vraie au rang 0 et elle est héréditaire donc elle est vraie pour tout entier naturel  .
.
3. Au bout de combien de minutes la stérilisation débute-elle ?
On résout l'inéquation 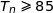 où
où  est un entier naturel.
est un entier naturel.

En appliquant la fonction logarithme (strictement croissante sur 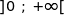 ) à chaque membre cela équivaut à :
) à chaque membre cela équivaut à :
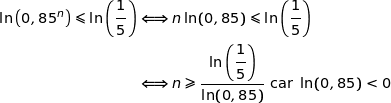
Avec 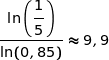 .
.
Donc la stérilisation débute au bout de 10 minutes.
Partie B : Modélisation continue
Dans cette partie, 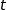 désigne un réel positif.
désigne un réel positif.
On suppose désormais qu'à l'instant 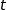 (exprimé en minutes), la température de la boîte est
donnée par
(exprimé en minutes), la température de la boîte est
donnée par 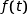 (exprimée en degré Celsius) avec :
(exprimée en degré Celsius) avec :
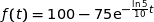
1.
a) Etudier le sens de variations de  sur
sur 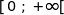 .
.
La fonction  est dérivable sur
est dérivable sur 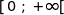 et nous avons :
et nous avons :
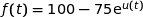
avec 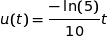 ;
; 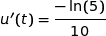
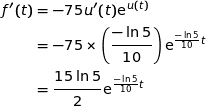
comme 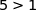 ;
; 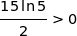 et pour tout
et pour tout 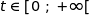 ,
, 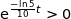 , donc
, donc 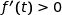 ce qui montre que
ce qui montre que  est strictement croissante sur
est strictement croissante sur 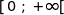 .
.
b) Justifier que si 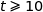 alors
alors 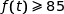 .
.
Comme  est croissante, si
est croissante, si 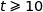 , alors
, alors 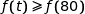 ; or :
; or :
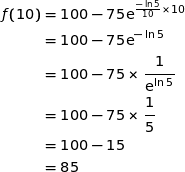
ce qui donne bien 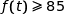 .
.
2. Soit 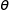 un réel supérieur ou égal à 10.
un réel supérieur ou égal à 10.
On note 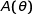 le domaine délimité par les droites d'équation
le domaine délimité par les droites d'équation 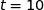 ,
, 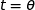 ,
, 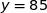 et la courbe représentative
et la courbe représentative 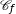 de
de  .
.
On considère que la stérilisation est finie au bout d'un temps 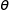 , si l'aire, exprimée en unité
d'aire du domaine
, si l'aire, exprimée en unité
d'aire du domaine 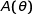 est supérieure à
est supérieure à 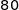 .
.
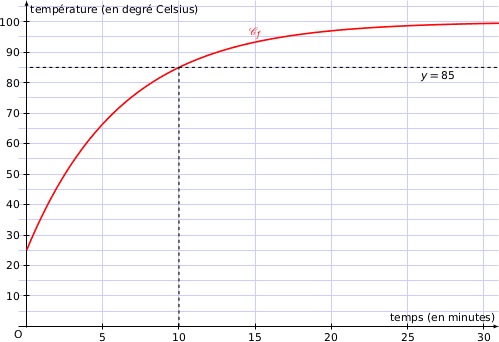
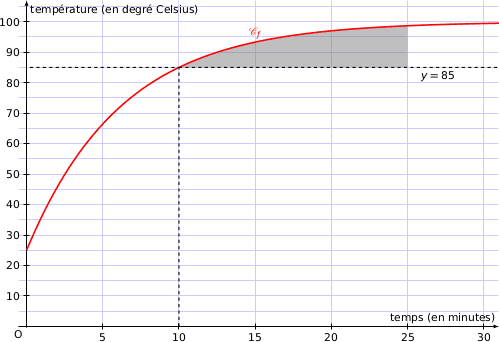
a) Justifier, à l'aide du graphique, que l'on a 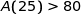 .
.
Sur le graphique chaque rectangle de la grille du repère représente 25 u.a. On évalue par lecture graphique que l'aire du domaine considéré est supérieure à l'aire de 4 rectangles soit supérieure à 100 u.a. donc 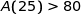 .
.
b) Justifier que, pour 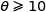 , on a
, on a 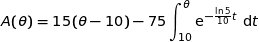 .
.
Pour tout 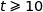 ;
; 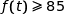 donc
donc 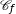 est située au dessus de la droite d'équation
est située au dessus de la droite d'équation 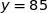 . Par conséquent pour
. Par conséquent pour 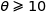 :
:
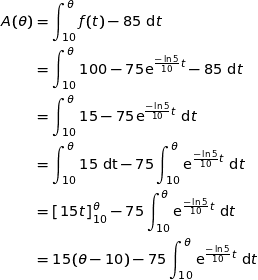
c) La stérilisation est-elle finie au bout de 20 minutes ?
On calcule 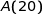 :
:
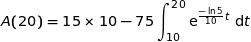
Une primitive sur 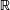 de la fonction
de la fonction 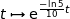 est
est 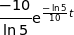 .
.
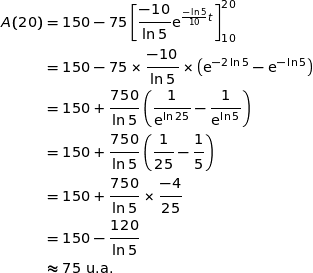
Donc la stérilisation n'est pas terminée au bout de 20 minutes puisque 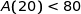 .
.
