Corrigé de l'exercice 2 de maths du bac S de mai 2012 en Amérique du nord
Cacher les corrigés
Partie A : Restitution organisée de connaissances
On rappelle que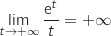 .
Démontrer que
.
Démontrer que 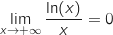 .
.
Pour tout 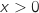 , on considère l'expression
, on considère l'expression 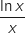 .
Posons
.
Posons 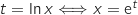 .
On a
.
On a 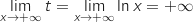 .
Du coup on a :
.
Du coup on a :
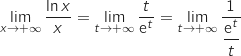 .
En utilisant le prérequis et par inverse on obtient le résultat 0.
.
En utilisant le prérequis et par inverse on obtient le résultat 0.
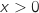 , on considère l'expression
, on considère l'expression 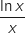 .
Posons
.
Posons 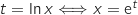 .
On a
.
On a 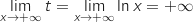 .
Du coup on a :
.
Du coup on a :
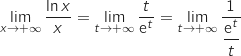 .
En utilisant le prérequis et par inverse on obtient le résultat 0.
.
En utilisant le prérequis et par inverse on obtient le résultat 0.
Partie B
On considère la fonction définie sur
définie sur 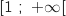 par
par
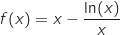
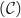 sa courbe représentative dans un repère orthonormal
sa courbe représentative dans un repère orthonormal 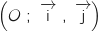 .
1. Soit
.
1. Soit  la fonction définie sur
la fonction définie sur 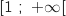 par
par
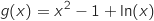
 est positive sur
est positive sur 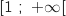 .
.
Pour tout 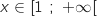 ,
, 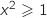 , donc
, donc  et de même
et de même 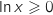 .
Donc
.
Donc 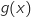 (qui est la somme de
(qui est la somme de 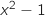 et
et 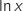 ) est également positif.
) est également positif.
2.a. Montrer que, pour tout 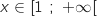 ,
, 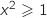 , donc
, donc  et de même
et de même 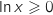 .
Donc
.
Donc 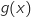 (qui est la somme de
(qui est la somme de 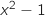 et
et 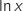 ) est également positif.
) est également positif.
 de
de 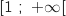 ,
, 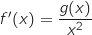 .
.
La fonction  est définie et dérivable sur
est définie et dérivable sur 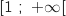 et on a :
et on a :
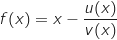 , avec :
, avec :
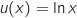
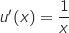
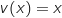
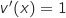
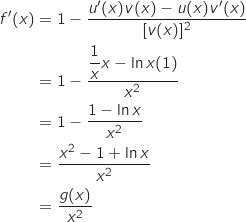
 est définie et dérivable sur
est définie et dérivable sur 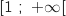 et on a :
et on a :
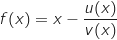 , avec :
, avec :
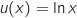
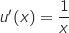
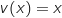
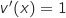
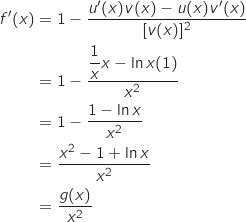
b. En déduire le sens de variation de
 sur
sur 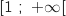 .
.
Pour 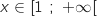 , le signe de
, le signe de  est le même que celui de
est le même que celui de 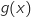 .
On a vu que pour tout
.
On a vu que pour tout 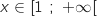 ,
, 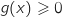 (et
(et 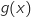 ne s'annule que pour
ne s'annule que pour  ), on en déduit que
), on en déduit que  est strictement croissante sur
est strictement croissante sur 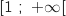 .
.
c. On considère la droite 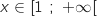 , le signe de
, le signe de  est le même que celui de
est le même que celui de 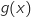 .
On a vu que pour tout
.
On a vu que pour tout 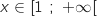 ,
, 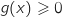 (et
(et 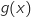 ne s'annule que pour
ne s'annule que pour  ), on en déduit que
), on en déduit que  est strictement croissante sur
est strictement croissante sur 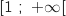 .
.
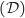 d'équation
d'équation 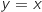 .
.
Dans l'énoncé original il faut établir que  est une asymptote oblique à la courbe
est une asymptote oblique à la courbe  .
La notion d'asymptote oblique est hors programme à compter de la rentrée scolaire 2012.
.
La notion d'asymptote oblique est hors programme à compter de la rentrée scolaire 2012.
d. Etudier la position de la courbe  est une asymptote oblique à la courbe
est une asymptote oblique à la courbe  .
La notion d'asymptote oblique est hors programme à compter de la rentrée scolaire 2012.
.
La notion d'asymptote oblique est hors programme à compter de la rentrée scolaire 2012.
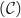 par rapport à la droite
par rapport à la droite 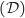 .
.
On étudie le signe de 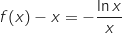 .
Pour
.
Pour 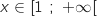 , le signe de l'expression est le même que celui de
, le signe de l'expression est le même que celui de 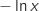 soit négatif (et nul pour
soit négatif (et nul pour  ).
On en déduit que :
).
On en déduit que :
3. Pour tout entier naturel 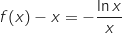 .
Pour
.
Pour 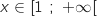 , le signe de l'expression est le même que celui de
, le signe de l'expression est le même que celui de 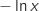 soit négatif (et nul pour
soit négatif (et nul pour  ).
On en déduit que :
).
On en déduit que :
- pour
 ,
, 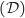 et
et 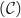 se coupent,
se coupent,
- pour
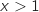 ,
, 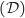 est au dessus de
est au dessus de  .
.
 supérieur ou égal à 2, on note
respectivement
supérieur ou égal à 2, on note
respectivement 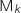 et
et 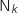 les points d'abscisse
les points d'abscisse  de
de 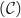 et
et 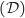 .
a. Montrer que, pour tout entier naturel
.
a. Montrer que, pour tout entier naturel  supérieur ou égal à 2, la distance
supérieur ou égal à 2, la distance 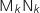 entre les points
entre les points 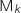 et
et 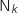 est
donnée par
est
donnée par 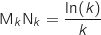 .
.
Comme on vient de voir que pour tout 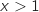 ,
, 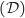 est au dessus de
est au dessus de 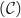 on en déduit que pour tout entier
on en déduit que pour tout entier 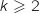 on a :
on a :
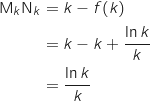
b. Ecrire un algorithme déterminant le plus petit entier 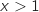 ,
, 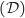 est au dessus de
est au dessus de 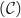 on en déduit que pour tout entier
on en déduit que pour tout entier 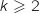 on a :
on a :
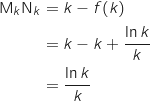
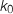 supérieur ou égal à 2 tel que la distance
supérieur ou égal à 2 tel que la distance 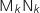 soit inférieur ou égale à
soit inférieur ou égale à 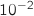 .
.
Variables
k : nombre entier
distance : nombre réel
Initialisation
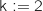
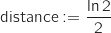 Traitement
Tant que distance
Traitement
Tant que distance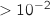 faire
faire
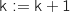
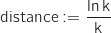 Fin Tant que
Sortie
Afficher k
Fin Tant que
Sortie
Afficher k
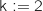
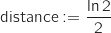 Traitement
Tant que distance
Traitement
Tant que distance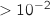 faire
faire
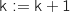
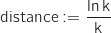 Fin Tant que
Sortie
Afficher k
Fin Tant que
Sortie
Afficher k
