Corrigé de l'exercice 3 du bac S de maths de mai 2012 en Amérique du nord
Cacher les corrigés
Cet exercice est complétement hors programme à compter de la session 2013 du baccalauréat.
Soit  une fonction définie et dérivable sur
une fonction définie et dérivable sur  telle
que :
telle
que :
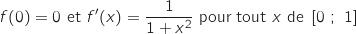
 .
.
Partie A
1. Déterminer le sens de variation de sur
sur  .
.
De manière évidente, pour tout 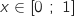 , on a
, on a 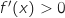 , donc
, donc  est strictement croissante sur
est strictement croissante sur  .
.
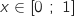 , on a
, on a 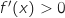 , donc
, donc  est strictement croissante sur
est strictement croissante sur  .
.
2. Soit
 la fonction définie sur
la fonction définie sur 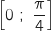 par
par 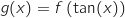 .
a. Justifier que
.
a. Justifier que  est dérivable sur
est dérivable sur 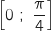 , puis que,
pour tout
, puis que,
pour tout  de
de 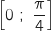 ,
, 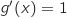 .
.
La fonction  est composée de la fonction
est composée de la fonction 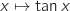 définie et dérivable sur
définie et dérivable sur 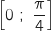 à valeurs dans
à valeurs dans  suivie de la fonction
suivie de la fonction
 définie et dérivable sur
définie et dérivable sur  , donc
, donc  est définie et dérivable sur
est définie et dérivable sur 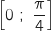 .
En utilisant la formule de la dérivée d'une composée on a pour tout
.
En utilisant la formule de la dérivée d'une composée on a pour tout 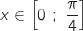 :
:
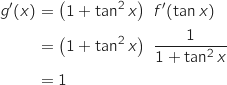
 est composée de la fonction
est composée de la fonction 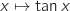 définie et dérivable sur
définie et dérivable sur 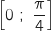 à valeurs dans
à valeurs dans  suivie de la fonction
suivie de la fonction
 définie et dérivable sur
définie et dérivable sur  , donc
, donc  est définie et dérivable sur
est définie et dérivable sur 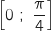 .
En utilisant la formule de la dérivée d'une composée on a pour tout
.
En utilisant la formule de la dérivée d'une composée on a pour tout 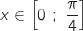 :
:
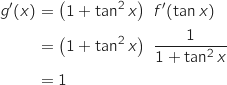
b. Montrer que, pour tout
 de
de 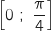 ,
, 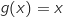 , en
déduire que
, en
déduire que 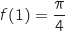 .
.
La fonction  est une primitive de la fonction constante 1, donc
est une primitive de la fonction constante 1, donc 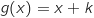 avec
avec 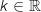 .
Comme
.
Comme 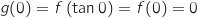 , on a
, on a 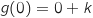 , soit
, soit 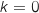 .
Donc finalement,
.
Donc finalement, 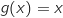 .
On calcule maintenant :
.
On calcule maintenant :
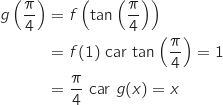 Du coup,
Du coup, 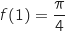 .
.
3. Montrer que, pour tout  est une primitive de la fonction constante 1, donc
est une primitive de la fonction constante 1, donc 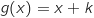 avec
avec 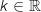 .
Comme
.
Comme 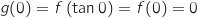 , on a
, on a 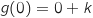 , soit
, soit 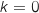 .
Donc finalement,
.
Donc finalement, 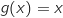 .
On calcule maintenant :
.
On calcule maintenant :
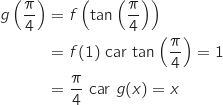 Du coup,
Du coup, 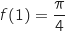 .
.
 de
de  ,
, 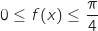 .
.
On a vu que  est strictement croissante donc :
est strictement croissante donc :
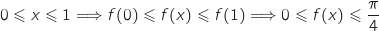 .
.
 est strictement croissante donc :
est strictement croissante donc :
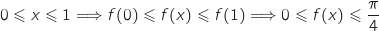 .
.
Partie B
Soit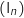 la suite définie par
la suite définie par 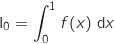 et, pour tout entier naturel
et, pour tout entier naturel  non nul,
non nul,
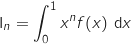 .
1. Montrer à l'aide d'une intégration par parties que,
.
1. Montrer à l'aide d'une intégration par parties que, 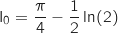 .
.
Pour calculer 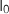 , on pose :
, on pose :
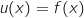
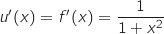
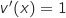
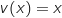 .
Les fonctions
.
Les fonctions  et
et  qui interviennent sont définies et dérivables sur
qui interviennent sont définies et dérivables sur  et à dérivées continues donc on a d'après
la formule d'intégration par parties :
et à dérivées continues donc on a d'après
la formule d'intégration par parties :
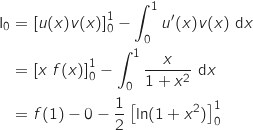 car
car 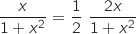 et comme sur
et comme sur  la fonction
la fonction  est strictement positive, une primitive de
est strictement positive, une primitive de
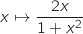 est
est 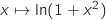 .
Pour finir :
.
Pour finir :
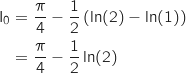
2.a. Montrer que, pour tout entier naturel non nul 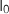 , on pose :
, on pose :
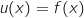
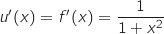
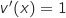
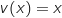 .
Les fonctions
.
Les fonctions  et
et  qui interviennent sont définies et dérivables sur
qui interviennent sont définies et dérivables sur  et à dérivées continues donc on a d'après
la formule d'intégration par parties :
et à dérivées continues donc on a d'après
la formule d'intégration par parties :
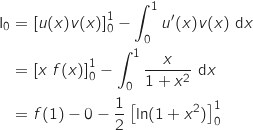 car
car 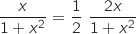 et comme sur
et comme sur  la fonction
la fonction  est strictement positive, une primitive de
est strictement positive, une primitive de
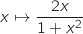 est
est 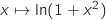 .
Pour finir :
.
Pour finir :
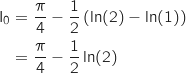
 ,
, 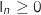 .
.
Pour tout 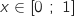 et tout entier naturel
et tout entier naturel 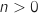 , on a :
, on a :
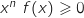 et
et 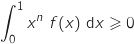 .
.
b. Montrer que, pour tout entier naturel non nul 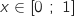 et tout entier naturel
et tout entier naturel 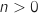 , on a :
, on a :
-
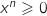 ,
,
-
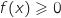 (question A.3.).
(question A.3.).
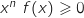 et
et 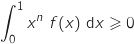 .
.
 ,
, 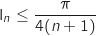 .
.
On a vu (question A.3.) que pour tout 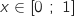 ,
, 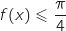 et donc
et donc 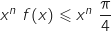 .
L'intégration conserve l'ordre (quand la borne basse est inférieur à la borne haute, ce qui est le cas ici), donc :
.
L'intégration conserve l'ordre (quand la borne basse est inférieur à la borne haute, ce qui est le cas ici), donc :
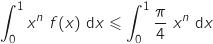
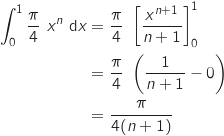 Donc on a bien,
Donc on a bien, 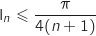 .
.
c. En déduire la limite de la suite 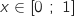 ,
, 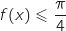 et donc
et donc 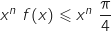 .
L'intégration conserve l'ordre (quand la borne basse est inférieur à la borne haute, ce qui est le cas ici), donc :
.
L'intégration conserve l'ordre (quand la borne basse est inférieur à la borne haute, ce qui est le cas ici), donc :
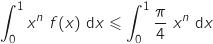
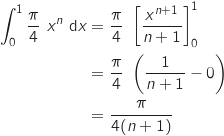 Donc on a bien,
Donc on a bien, 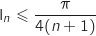 .
.
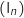 .
.
Soit la suite  définie pour tout entier
définie pour tout entier 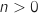 , par
, par 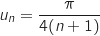 .
On a
.
On a 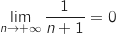 et par produit
et par produit 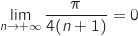 .
Du coup,
.
Du coup, 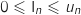 avec
avec 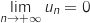 .
Donc d'après le théorème des gendarmes la suite
.
Donc d'après le théorème des gendarmes la suite 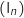 converge vers 0.
converge vers 0.
 définie pour tout entier
définie pour tout entier 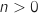 , par
, par 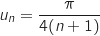 .
On a
.
On a 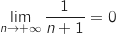 et par produit
et par produit 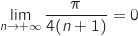 .
Du coup,
.
Du coup, 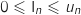 avec
avec 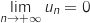 .
Donc d'après le théorème des gendarmes la suite
.
Donc d'après le théorème des gendarmes la suite 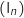 converge vers 0.
converge vers 0.
