Corrigé de l'exercice 4 du bac S de maths de mai 2012 en Amérique du nord
Cacher les corrigés
Le plan complexe est rapporté à un repère orthonormal direct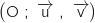 .
On considère l'application
.
On considère l'application  du plan dans lui même qui, à tout point
M d'affixe
du plan dans lui même qui, à tout point
M d'affixe  , associe le point M' d'affixe
, associe le point M' d'affixe 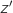 telle que :
telle que :
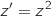
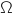 le point d'affixe
le point d'affixe 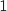 .
1. Déterminer l'ensemble
.
1. Déterminer l'ensemble 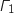 des points M du plan tels que
des points M du plan tels que 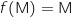 .
.
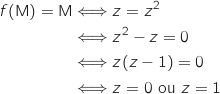 Donc l'ensemble
Donc l'ensemble 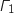 est constitué de deux points : O (origine du repère) et
est constitué de deux points : O (origine du repère) et 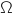 .
.
2. Soit A le point d'affixe
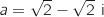 .
a. Exprimer
.
a. Exprimer  sous forme exponentielle.
sous forme exponentielle.
Le module de  est
est 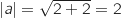 , et on peut écrire :
, et on peut écrire :
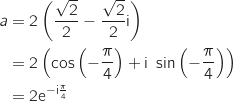
b. En déduire les affixes des deux antécédents de A par  est
est 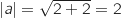 , et on peut écrire :
, et on peut écrire :
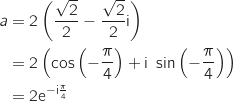
 .
.
On cherche 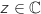 , tel que :
, tel que :
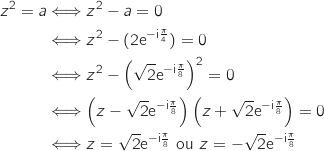
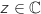 , tel que :
, tel que :
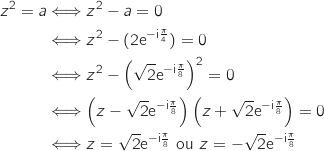
3. Déterminer l'ensemble
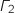 des points M d'affixe
des points M d'affixe  tels que l'affixe
tels que l'affixe 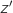 du point M' soit un nombre imaginaire pur.
du point M' soit un nombre imaginaire pur.
On cherche 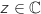 , tel que
, tel que 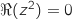 .
Posons
.
Posons 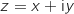 où
où  et
et 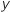 sont des nombres réels.
sont des nombres réels.
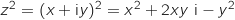 , donc
, donc 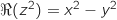 .
Du coup l'ensemble
.
Du coup l'ensemble 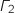 des points M
des points M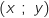 cherchés a pour équation cartésienne :
cherchés a pour équation cartésienne :
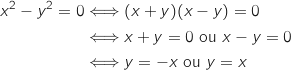 Donc
Donc 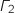 est constitué de la réunion des points des droites d'équations
est constitué de la réunion des points des droites d'équations 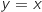 et
et 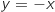 .
.
4. Dans cette question, on souhaite déterminer l'ensemble
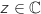 , tel que
, tel que 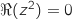 .
Posons
.
Posons 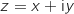 où
où  et
et 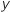 sont des nombres réels.
sont des nombres réels.
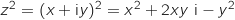 , donc
, donc 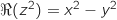 .
Du coup l'ensemble
.
Du coup l'ensemble 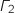 des points M
des points M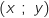 cherchés a pour équation cartésienne :
cherchés a pour équation cartésienne :
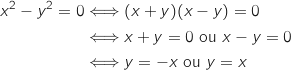 Donc
Donc 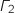 est constitué de la réunion des points des droites d'équations
est constitué de la réunion des points des droites d'équations 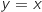 et
et 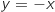 .
.
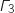 des points M distincts de
des points M distincts de 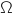 pour lesquels le
triangle
pour lesquels le
triangle 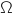 MM' est rectangle isocèle direct en
MM' est rectangle isocèle direct en 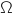 .
a. On admet que M est un point de
.
a. On admet que M est un point de 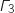 si et
seulement si
si et
seulement si 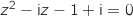 et
et 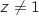 .
.
Dans le sujet original la relation indiquée doit être établie en utilisant une rotation.
Depuis la rentrée 2012, les rotations ne sont plus au programme.
b. Montrer que 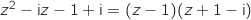 .
.
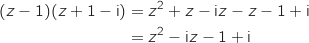
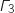 .
.
En utilisant les deux questions précédentes M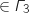 équvaut à :
équvaut à :
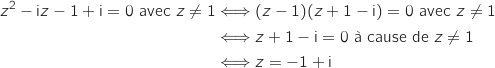 Donc l'ensemble
Donc l'ensemble 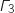 est constitué d'un unique point, le point d'affixe
est constitué d'un unique point, le point d'affixe 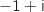 .
.
5. Soit M un point d'affixe 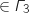 équvaut à :
équvaut à :
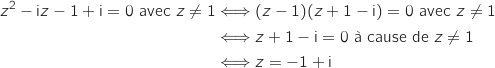 Donc l'ensemble
Donc l'ensemble 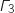 est constitué d'un unique point, le point d'affixe
est constitué d'un unique point, le point d'affixe 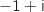 .
.
 différente de
différente de 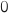 et de
et de 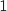 .
a. Exprimer
.
a. Exprimer 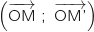 en fonction d'un argument de
en fonction d'un argument de  .
.
Pour 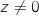 et
et 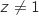 on a :
on a :
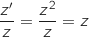 donc
donc 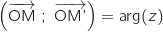 .
.
b. En déduire l'ensemble 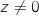 et
et 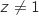 on a :
on a :
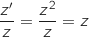 donc
donc 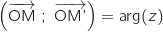 .
.
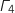 des points M distincts de
O et de
des points M distincts de
O et de 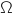 tels que O, M et M' soient alignés.
tels que O, M et M' soient alignés.
Pour tout point M d'affixe  , distinct de O et
, distinct de O et 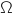 , O, M et M' sont alignés équivaut à
, O, M et M' sont alignés équivaut à
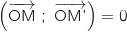 ou
ou 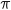 , soit
, soit 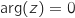 ou
ou 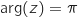 .
Donc l'ensemble
.
Donc l'ensemble 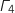 est constitué des points de l'axe des abscisses privé de O et
est constitué des points de l'axe des abscisses privé de O et 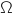 .
.
 , distinct de O et
, distinct de O et 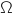 , O, M et M' sont alignés équivaut à
, O, M et M' sont alignés équivaut à
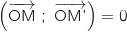 ou
ou 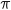 , soit
, soit 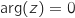 ou
ou 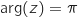 .
Donc l'ensemble
.
Donc l'ensemble 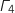 est constitué des points de l'axe des abscisses privé de O et
est constitué des points de l'axe des abscisses privé de O et 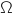 .
.
