Sujet et corrigé de l'exercice 1 du bac S de maths de mai 2013 en Amérique du nord
Cacher les corrigés
On se place dans l'espace muni d'un repère orthonormé. On considère les points A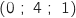 , B
, B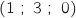 , C
, C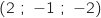 et D
et D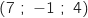 .
.
1. Démontrer que les points A, B et C ne sont pas alignés.
On calcule, par exemple, les coordonnées des vecteurs 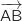 et
et 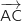 :
:
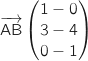
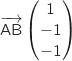
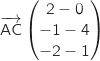
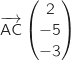 Les coordonnées de ces vecteurs ne sont pas proportionnelles donc ils ne sont pas colinéaires ce qui montre que les points A, B et C ne sont pas alignés.
Les coordonnées de ces vecteurs ne sont pas proportionnelles donc ils ne sont pas colinéaires ce qui montre que les points A, B et C ne sont pas alignés.
2. Soit 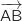 et
et 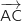 :
:
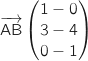
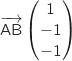
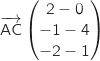
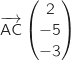 Les coordonnées de ces vecteurs ne sont pas proportionnelles donc ils ne sont pas colinéaires ce qui montre que les points A, B et C ne sont pas alignés.
Les coordonnées de ces vecteurs ne sont pas proportionnelles donc ils ne sont pas colinéaires ce qui montre que les points A, B et C ne sont pas alignés.
 la droite passant par le point D et de vecteur directeur
la droite passant par le point D et de vecteur directeur 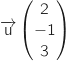 .
a. Démontrer que la droite
.
a. Démontrer que la droite  est orthogonale au plan (ABC).
est orthogonale au plan (ABC).
Les vecteurs 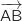 et
et 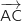 ci-dessus sont deux vecteurs non colinéaires du plan, de plus on a :
ci-dessus sont deux vecteurs non colinéaires du plan, de plus on a :
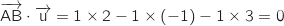
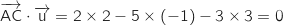 Du coup
Du coup 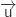 est orthogonal aux vecteurs
est orthogonal aux vecteurs 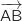 et
et 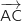 ce qui entraîne que
ce qui entraîne que
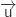 est un vecteur normal au plan (ABC) et que la droite
est un vecteur normal au plan (ABC) et que la droite  est orthogonale à ce plan.
est orthogonale à ce plan.
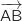 et
et 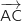 ci-dessus sont deux vecteurs non colinéaires du plan, de plus on a :
ci-dessus sont deux vecteurs non colinéaires du plan, de plus on a :
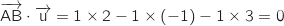
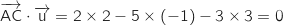 Du coup
Du coup 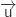 est orthogonal aux vecteurs
est orthogonal aux vecteurs 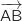 et
et 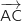 ce qui entraîne que
ce qui entraîne que
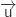 est un vecteur normal au plan (ABC) et que la droite
est un vecteur normal au plan (ABC) et que la droite  est orthogonale à ce plan.
est orthogonale à ce plan.
b. En déduire une équation cartésienne du plan (ABC).
Comme 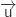 est un vecteur normal au plan (ABC), ce plan admet une équation cartésienne de la forme :
est un vecteur normal au plan (ABC), ce plan admet une équation cartésienne de la forme :
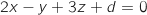
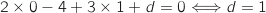 Donc une équation cartésienne du plan (ABC) est
Donc une équation cartésienne du plan (ABC) est 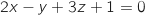
c. Déterminer une représentation paramétrique de la droite 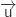 est un vecteur normal au plan (ABC), ce plan admet une équation cartésienne de la forme :
est un vecteur normal au plan (ABC), ce plan admet une équation cartésienne de la forme :
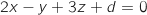
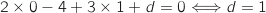 Donc une équation cartésienne du plan (ABC) est
Donc une équation cartésienne du plan (ABC) est 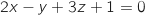
 .
.
En utilisant le point D et le vecteur 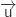 on peut donner directement une représentation paramétrique de la droite en question :
on peut donner directement une représentation paramétrique de la droite en question :
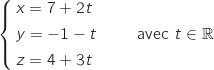
d. Déterminer les coordonnées du point H, intersection de la droite 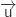 on peut donner directement une représentation paramétrique de la droite en question :
on peut donner directement une représentation paramétrique de la droite en question :
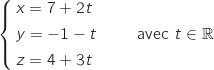
 et du plan (ABC).
et du plan (ABC).
Il s'agit de résoudre le système :
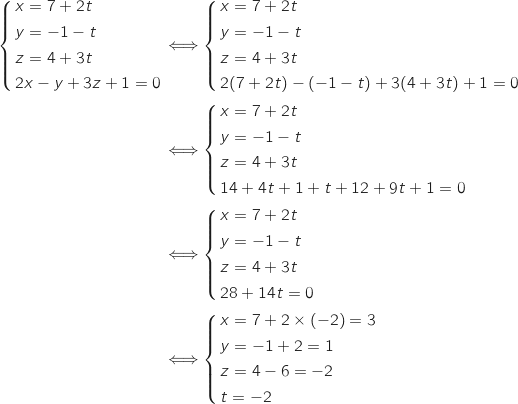 Donc H
Donc H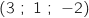 .
.
3. Soit 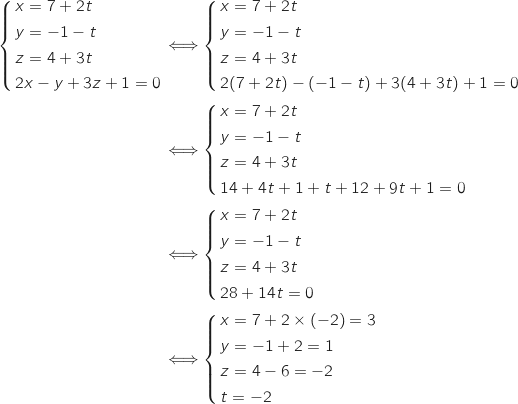 Donc H
Donc H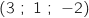 .
.
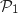 le plan d'équation
le plan d'équation 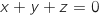 et
et 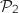 le plan d'équation
le plan d'équation 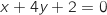 .
a. Démontrer que les plans
.
a. Démontrer que les plans 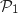 et
et 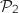 sont sécants.
sont sécants.
Par lecture directe sur les équations cartésiennes on trouve des vecteurs normaux 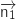 et
et 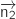 de
de
 et
et  :
:
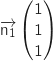
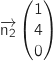 On remarque que ces vecteurs ne sont pas colinéaires donc les plans
On remarque que ces vecteurs ne sont pas colinéaires donc les plans  et
et  ne sont pas parallèles et par conséquent ils sont sécants.
ne sont pas parallèles et par conséquent ils sont sécants.
b. Vérifier que la droite  et
et 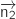 de
de
 et
et  :
:
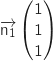
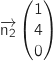 On remarque que ces vecteurs ne sont pas colinéaires donc les plans
On remarque que ces vecteurs ne sont pas colinéaires donc les plans  et
et  ne sont pas parallèles et par conséquent ils sont sécants.
ne sont pas parallèles et par conséquent ils sont sécants.
 , intersection des plans
, intersection des plans 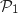 et
et 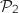 , a pour représentation paramétrique
, a pour représentation paramétrique
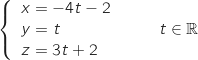 .
.
Les points de la droite 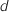 sont les points dont les coordonnées sont
sont les points dont les coordonnées sont 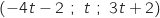 , on vérifie que ces points appartiennent
aux deux plans à l'aide des équations cartésiennes.
Pour
, on vérifie que ces points appartiennent
aux deux plans à l'aide des équations cartésiennes.
Pour 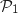 :
:
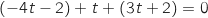 Pour
Pour 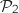 :
:
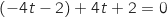 Donc
Donc 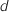 est bien la droite d'intersection des deux plans.
est bien la droite d'intersection des deux plans.
c. La droite 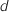 sont les points dont les coordonnées sont
sont les points dont les coordonnées sont 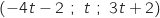 , on vérifie que ces points appartiennent
aux deux plans à l'aide des équations cartésiennes.
Pour
, on vérifie que ces points appartiennent
aux deux plans à l'aide des équations cartésiennes.
Pour 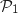 :
:
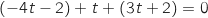 Pour
Pour 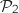 :
:
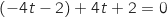 Donc
Donc 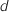 est bien la droite d'intersection des deux plans.
est bien la droite d'intersection des deux plans.
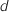 et le plan (ABC) sont-ils sécants ou parallèles ?
et le plan (ABC) sont-ils sécants ou parallèles ?
Par lecture sur la représentation paramétrique un vecteur directeur de 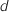 est
est 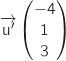 , on calcule
le produit scalaire avec le vecteur
, on calcule
le produit scalaire avec le vecteur 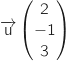 (vecteur normal à (ABC)) ce qui donne :
(vecteur normal à (ABC)) ce qui donne :
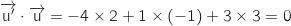 Donc
Donc 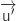 et
et 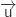 sont orthogonaux ce qui montre que la droite
sont orthogonaux ce qui montre que la droite 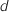 est parallèle au plan (ABC).
est parallèle au plan (ABC).
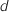 est
est 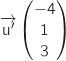 , on calcule
le produit scalaire avec le vecteur
, on calcule
le produit scalaire avec le vecteur 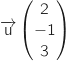 (vecteur normal à (ABC)) ce qui donne :
(vecteur normal à (ABC)) ce qui donne :
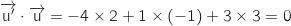 Donc
Donc 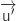 et
et 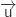 sont orthogonaux ce qui montre que la droite
sont orthogonaux ce qui montre que la droite 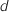 est parallèle au plan (ABC).
est parallèle au plan (ABC).
