Sujet et corrigé de l'exercice 3 du bac S de maths de mai 2013 en Amérique du nord
Cacher les corrigés
Une boulangerie industrielle utilise une machine pour fabriquer des pains de campagne pesant en moyenne 400 grammes. Pour être vendus aux clients, ces pains doivent peser au moins 385 grammes. Un pain dont la masse est strictement inférieure à 385 grammes est un pain non-commercialisable, un pain dont la masse est supérieure ou égale à 385 grammes est commercialisable. La masse d'un pain fabriqué par la machine peut être modélisée par une variable aléatoire suivant la loi normale d'espérance
suivant la loi normale d'espérance  et d'écart-type
et d'écart-type  .
Les probabilités seront arrondies au millième le plus proche
.
Les probabilités seront arrondies au millième le plus proche
Partie A
On pourra utiliser le tableau suivant dans lequel les valeurs sont arrondies au millième le plus proche.
 .
.
 (en utilisant les valeurs du tableau).
(en utilisant les valeurs du tableau).
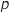 qu'un pain choisi au hasard dans la production soit commercialisable.
qu'un pain choisi au hasard dans la production soit commercialisable.
On sait qu'un pain est commercialisable s'il pèse au moins 385 g donc on calcule :


3. Le fabricant trouve cette probabilité
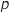 trop faible.
Il décide de modifier ses méthodes de production afin de faire varier la valeur de
trop faible.
Il décide de modifier ses méthodes de production afin de faire varier la valeur de 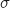 sans modifier celle de
sans modifier celle de 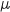 .
Pour quelle valeur de
.
Pour quelle valeur de 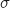 la probabilité qu'un pain soit commercialisable est-elle égale à 96 % ? On arrondira le résultat au dixième.
On pourra utiliser le résultat suivant : lorsque
la probabilité qu'un pain soit commercialisable est-elle égale à 96 % ? On arrondira le résultat au dixième.
On pourra utiliser le résultat suivant : lorsque 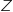 est une variable aléatoire qui suit la loi normale d'espérance
est une variable aléatoire qui suit la loi normale d'espérance 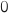 et d'écart-type 1, on a
et d'écart-type 1, on a  .
.
La variable aléatoire 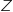 centrée réduite associée à
centrée réduite associée à  est définie par
est définie par  .
Comme
.
Comme 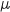 n'est pas modifiée cela donne
n'est pas modifiée cela donne  .
En outre on sait que
.
En outre on sait que 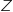 suit la loi normale centrée réduite.
On cherche
suit la loi normale centrée réduite.
On cherche 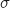 tel que :
tel que :
 D'après le résultat donné dans l'énoncé on en déduit que :
D'après le résultat donné dans l'énoncé on en déduit que :
 .
.
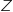 centrée réduite associée à
centrée réduite associée à  est définie par
est définie par  .
Comme
.
Comme 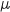 n'est pas modifiée cela donne
n'est pas modifiée cela donne  .
En outre on sait que
.
En outre on sait que 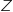 suit la loi normale centrée réduite.
On cherche
suit la loi normale centrée réduite.
On cherche 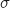 tel que :
tel que :
 D'après le résultat donné dans l'énoncé on en déduit que :
D'après le résultat donné dans l'énoncé on en déduit que :
 .
.
Partie B
Les méthodes de production ont été modifiées dans le but d'obtenir 96 % de pains commercialisables. Afin d'évaluer l'efficacité de ces modifications, on effectue un contrôle qualité sur un échantillon de 300 pains fabriqués. 1. Déterminer l'intervalle de fluctuation asymptotique au seuil de 95 % de la proportion de pains commercialisables dans un échantillon de taille 300.
On utilise la « formule » du cours :

 et
et  .
On peut déjà vérifier que les conditions usuelles d'utilisation sont satisfaites :
.
On peut déjà vérifier que les conditions usuelles d'utilisation sont satisfaites :
 et l'intervalle demandé est :
et l'intervalle demandé est :
 soit
soit  .
.
2. Parmi les 300 pains de l'échantillon, 283 sont commercialisables.
Au regard de l'intervalle de fluctuation obtenu à la question 1, peut-on décider que l'objectif a été atteint ?

 et
et  .
On peut déjà vérifier que les conditions usuelles d'utilisation sont satisfaites :
.
On peut déjà vérifier que les conditions usuelles d'utilisation sont satisfaites :
-
 ; donc
; donc 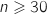
-
 ; donc
; donc 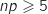
-
 ; donc
; donc 
 et l'intervalle demandé est :
et l'intervalle demandé est :
 soit
soit  .
.
La proportion de pains commercialisables observée dans l'échantillon est  .
Cette valeur appartient à l'intervalle de fluctuation dont on peut décider que l'objectif est atteint.
.
Cette valeur appartient à l'intervalle de fluctuation dont on peut décider que l'objectif est atteint.
 .
Cette valeur appartient à l'intervalle de fluctuation dont on peut décider que l'objectif est atteint.
.
Cette valeur appartient à l'intervalle de fluctuation dont on peut décider que l'objectif est atteint.
Partie C
Le boulanger utilise une balance électronique. Le temps de fonctionnement sans dérèglement, en jours, de cette balance électronique est une variable aléatoire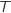 qui suit une loi exponentielle de paramètre
qui suit une loi exponentielle de paramètre 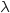 .
1. On sait que la probabilité que la balance électronique ne se dérègle pas avant 30 jours est de
.
1. On sait que la probabilité que la balance électronique ne se dérègle pas avant 30 jours est de  . En déduire la valeur de
. En déduire la valeur de 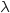 arrondie au millième.
arrondie au millième.
La variable aléatoire 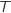 suit une loi exponentielle de paramètre
suit une loi exponentielle de paramètre 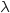 dont la fonction de densité est la fonction :
dont la fonction de densité est la fonction :  , du coup
pour tout réel
, du coup
pour tout réel  :
:
 Les données de l'énoncé permettent d'écrire :
Les données de l'énoncé permettent d'écrire :

Dans toute la suite on prendra 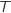 suit une loi exponentielle de paramètre
suit une loi exponentielle de paramètre 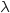 dont la fonction de densité est la fonction :
dont la fonction de densité est la fonction :  , du coup
pour tout réel
, du coup
pour tout réel  :
:
 Les données de l'énoncé permettent d'écrire :
Les données de l'énoncé permettent d'écrire :

 .
2. Quelle est la probabilité que la balance électronique fonctionne encore sans dérèglement après 90 jours, sachant qu'elle a fonctionné sans dérèglement 60 jours ?
.
2. Quelle est la probabilité que la balance électronique fonctionne encore sans dérèglement après 90 jours, sachant qu'elle a fonctionné sans dérèglement 60 jours ?
On cherche :
 car la variable aléatoire
car la variable aléatoire 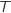 vérifie la propriété de durée de vie sans vieillissement puisqu'elle suit une loi exponentielle.
vérifie la propriété de durée de vie sans vieillissement puisqu'elle suit une loi exponentielle.
3. Le vendeur de cette balance électronique a assuré au boulanger qu'il y avait une chance sur deux pour que la balance ne se dérègle pas avant un an.
A-t-il raison ? Si non, pour combien de jours est-ce vrai ?
 car la variable aléatoire
car la variable aléatoire 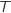 vérifie la propriété de durée de vie sans vieillissement puisqu'elle suit une loi exponentielle.
vérifie la propriété de durée de vie sans vieillissement puisqu'elle suit une loi exponentielle.
On calcule la probabilité que la balance fonctionne encore au bout d'un an :
 .
On obtient un résultat bien « loin » de 0,5 ; donc le vendeur n'a pas raison.
On cherche maintenant le nombre
.
On obtient un résultat bien « loin » de 0,5 ; donc le vendeur n'a pas raison.
On cherche maintenant le nombre  de jours tels que
de jours tels que  ce qui donne :
ce qui donne :
 Donc l'affirmation est vraie pour 231 jours environ.
Donc l'affirmation est vraie pour 231 jours environ.
 .
On obtient un résultat bien « loin » de 0,5 ; donc le vendeur n'a pas raison.
On cherche maintenant le nombre
.
On obtient un résultat bien « loin » de 0,5 ; donc le vendeur n'a pas raison.
On cherche maintenant le nombre  de jours tels que
de jours tels que  ce qui donne :
ce qui donne :
 Donc l'affirmation est vraie pour 231 jours environ.
Donc l'affirmation est vraie pour 231 jours environ.
