Sujet et corrigé de l'exercice 2 du bac S de maths de mai 2014 en Amérique du nord
Cacher les corrigés
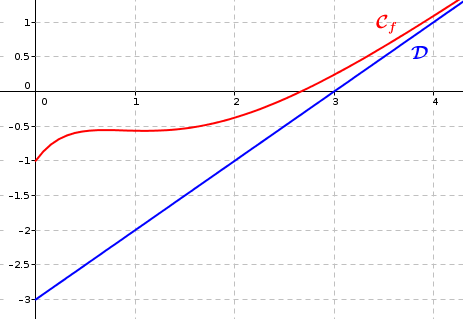
On considère la fonction définie sur par :
On note la représentation graphique de la fonction et la droite d'équation dans un repère orthogonal du plan.
Partie A : Positions relatives de et
Soit la fonction définie sur l'intervalle par :
1. Justifier, que pour tout réel de l'intervalle , .
Pour tout
Pour tout ,
Le signe de est le même que celui de .
On résout :
avec
Donc pour , ainsi que .
2. La courbe et la droite ont-elles un point commun ?
Justifier.
D'après ce qui précède, pour tout :
donc , ce qui montre que sur et n'ont pas de point commun.
Partie B : Etude de la fonction
On note le point d'abscisse de la courbe , le point d'abscisse de la droite et on s'intéresse à l'évolution de la distance .
1. Justifier que, pour tout de l'intervalle , la distance est égale à .
Les points et ont la même abscisse, donc est égale à la valeur absolue de la différence des ordonnées des points soit :
,
comme on a vu dans la partie A que sur l'intervalle , on a et donc .
2. On note la fonction dérivée de la fonction sur l'intervalle .
Pour tout de l'intervalle , calculer .
En faisant attention à bien dériver les composées on a pour tout :
3. Montrer que la fonction possède un maximum sur l'intervalle que l'on déterminera.
En donner une interprétation graphique.
On étudie le signe de .
On remarque déjà que
Du coup le signe de est le même que celui de (puisque ).
Il reste à résoudre, par exemple, l'inéquation :
où .
De même on aurait : et
.
Ainsi sur , la dérivée s'annule pour en changeant de signe du positif au négatif.
Cela montre que la fonction admet un maximum pour .
La valeur du maximum est :
La distance maximale entre et est et est atteinte pour .
Partie C : Etude d'une aire
On considère la fonction définie sur l'intervalle par :
1. Hachurer sur le graphique ci-dessous le domaine dont l'aire est donnée par .
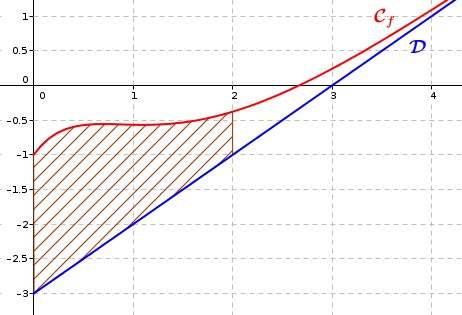
2. Justifier que la fonction est croissante sur l'intervalle .
On remarque .
La fonction est dérivable sur et pour tout de cet intervalle on a :
or on a vu que est positive sur ,
du coup pour tout , ce qui montre que est croissante.
3. Pour tout réel strictement positif, calculer .
4. Existe-t-il une valeur de telle que ?
On résout :
En posant , il vient :
Donc :
Comme et qu'on travaille sur , on en conclut qu'il existe une valeur de telle que et que cette valeur est .
