Sujet et corrigé de l'exercice 3 du bac S de maths de mai 2014 en Amérique du nord
Cacher les corrigés
On considère un cube ABCDEFGH donné ci-dessous :
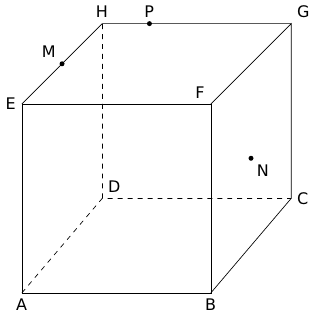
On note M le milieu du segment [EH], N celui de [FC] et P le point tel que .
Partie A : Section du cube par le plan (MNP)
1. Justifier que les droites (MP) et (FG) sont sécantes en un point L.
Construire le point L.
Dans le plan de la face EFGH, le point P n'est pas sur la parallèle à (FG) passant par M, donc (MP) n'est pas parallèle à (FG), c'est à dire que (MP) et (FG) se coupent.
2. On admet que les droites (LN) et (CG) sont sécantes et on note T leur point d'intersection.
On admet que les droite (LN) et (BF) sont sécantes et on note Q leur point d'intersection.
a. Construire les points T et Q en laissant apparent les traits de construction.
b. Construire l'intersection des plans (MNP) et (ABF).
3. En déduire une construction de la section du cube par le plan (MNP).
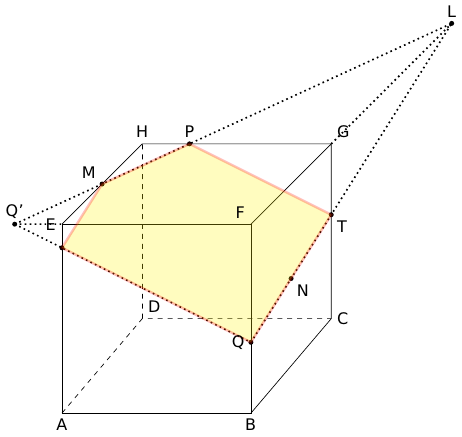
Partie B
L'espace est rapporté au repère .
1. Donner les coordonnées des points M, N et P dans ce repère.
2. Déterminer les coordonnées de L.
On détermine une représentation paramétrique de (MP) et de (FG).
soit
Donc une représentation paramétrique de (MP) est :
Donc une représentation paramétrique de (FG) est :
Pour trouver les coordonnées de L il s'agit de résoudre le système :
Donc
3. On admet que le point T a pour coordonnées .
Le triangle TPN est-il rectangle en T ?
On calcule :
On a :
Donc ce qui montre que le triangle n'est pas rectangle en T.
