Sujet et corrigé de l'exercice de spécialité du bac S de maths de mai 2014 en Amérique du nord
Cacher les corrigés
Un volume constant de 2 200 m d'eau est réparti entre deux bassins A et B.
Le bassin A refroidit une machine.
Pour des raisons d'équilibre thermique on crée un courant d'eau entre les deux bassins à l'aide de deux pompes.
On modélise les échanges entre les deux bassins de la façon suivante :
au départ, le bassin A contient d'eau et le bassin B contient d'eau ;
tous les jours, 15 % du volume d'eau présent en début de journée dans le bassin B est transféré vers le bassin A ;
tous les jours, 10 % du volume d'eau présent en début de journée dans le bassin A est transféré vers le bassin B, et, pour des raisons de maintenance, on transfère également 5 du bassin A vers le bassin B.
Pour tout entier naturel , on note :
le volume d'eau, exprimé en , contenu dans le bassin A à la fin du -ième jour de fonctionnement ;
le volume d'eau, exprimé en , contenu dans le bassin B à la fin du -ième jour de fonctionnement.
On a donc et .
1. Traduire la conservation du volume total d'eau du circuit par une relation liant et .
2. On utilise un tableur pour visualiser l'évolution du volume d'eau dans les bassins.
Donner les formules à écrire et à recopier vers le bas dans les cellules B3 et C3 permettant d'obtenir la feuille de calcul ci-dessous :
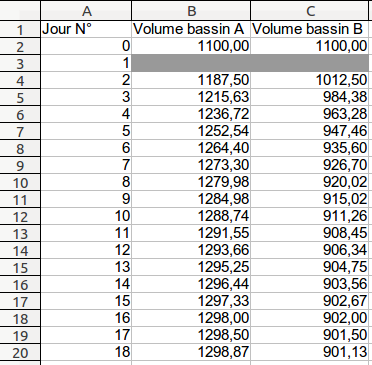
Bassin A : il reste 90 % du volume, 5 sont enlevés pour maintenance et 15 % du volume du bassin B est transféré donc on a la formule :
B3=0.9*B2-5+0.15*C2
Bassin B : il reste 85 % du volume, 5 sont ajoutés pour maintenance et 10 % du volume du bassin A est transféré donc on a la formule :
C3=0.85*C2+5+0.1*B2
3. Quelles conjectures peut-on faire sur l'évolution du volume d'eau dans chacun des bassins ?
On peut conjecturer qu'au fil des jours les volumes d'eau dans les bassins tendent à se stabiliser vers 1300 pour le bassin A et vers 900 pour le bassin B.
Partie B
On considère la matrice carrée et les matrices colonnes et .
On admet que, pour tout entier naturel , .
1. On note .
Vérifier que .
En déduire que, pour tout entier naturel , .
.
Pour tout entier naturel on a :
Dans la suite, on admettra que, pour tout entier naturel , et que :
2. Montrer que, pour tout entier naturel , .
De la relation , on obtient :
Donc :
3. Valider ou invalider les conjectures effectuées à la question 3. de la partie A.
Avec le résultat de la question précédente on a les formules explicites :
et
Comme , .
Et par conséquent : et .
Donc les conjectures effectuées dans la partie A sont valides.
4. On considère que le processus est stabilisé lorsque l'entier naturel vérifie :
Déterminer le premier jour pour lequel le processus est stabilisé.
On résout, par exemple :
où
donc le premier jour pour lequel le processus est stabilisé est le 18ème jour.
On notera qu'il n'y a pas besoin de résoudre en effet :
donc et
.
