Corrigé de l'exercice 1 du bac S de maths de novembre 2012 en Amérique du sud
Cacher les corrigés
Partie A
1. L'objet de cette question est de démontrer que
.
On suppose connus les résultats suivants :
- La fonction exponentielle est dérivable sur
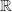et est égale à sa fonction dérivée.
-
.
- Pour tout réel
, on a 
.
- Soit deux fonctions
et 
définies sur l'intervalle 
, où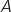 
est un réel positif.
Si pour tout de ,\: 
et si 
, alors 
.
1. Soit
la fonction définie sur 
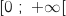par 
.
Montrer que pour tout de 
.
La fonction est dérivable sur 
et on a a : 
.
Pour tout réel , on sait que 
donc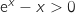 
soit 
.
On en déduit que est strictement croissante avec 
.
Donc pour tout 
, 
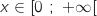c'est à dire 
.
On peut voir cela facilement sur le tableau de variations :
b. En déduire que est dérivable sur et on a a : .
Pour tout réel , on sait que donc 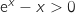soit .
On en déduit que est strictement croissante avec .
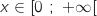Donc pour tout , c'est à dire .
On peut voir cela facilement sur le tableau de variations :
.
Pour tout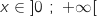 
:
Or 
, donc par comparaison : 
.
:
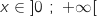Or , donc par comparaison : .
2. Soit
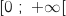la fonction définie sur par 
.
a. Etudier la limite de la fonction en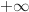 
.
On écrit 
b. Etudier les variations de la fonction
-
-
avec 
et par inverse : 
- Finalement, par composition :
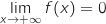(on peut poser 
).
, puis dresser son tableau de variations sur .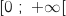
La fonction est dérivable sur et on a :
Le signe de la dérivée est le même que celui de 
et on a le tableau de variations :
est dérivable sur et on a :
Le signe de la dérivée est le même que celui de et on a le tableau de variations :
Partie B
Les questions 1 et 2 du sujet original traitent d'équations différentielles. Cette notion n'est plus au programme à partir de la rentrée 2012/2013.
3. On donne l'algorithme suivant :
est la fonction étudiée dans la partie A.
a. A l'aide de la question 2. a. de la partie A, expliquer pourquoi il est certain que cet algorithme donne une valeur en sortie.
Cet algorithme s'arête car .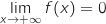
b. Quelle est la valeur .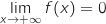
de la variable 
obtenue à la sortie de l'algorithme ?
L'algorithme retourne la première valeur entière 
telle que 
.
En utilisant la fonction table de la calculette on a 
et 
, donc 
.
telle que .
En utilisant la fonction table de la calculette on a et , donc .
