Corrigé de l'exercice 4 du bac S de maths de novembre 2012 en Amérique du sud
Cacher les corrigés
L'espace est muni d'un repère orthonormé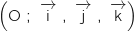 .
Soit
.
Soit  le plan d'équation cartésienne
le plan d'équation cartésienne 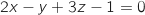 et soit S le point de coordonnées
et soit S le point de coordonnées 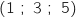 .
Pour chacune des affirmations suivantes, dire si elle est vraie ou fausse, et proposer une démonstration de la réponse indiquée.
.
Pour chacune des affirmations suivantes, dire si elle est vraie ou fausse, et proposer une démonstration de la réponse indiquée.
1. Les points d'intersection du plan
 avec les trois axes du repère sont les sommets d'un triangle isocèle.
avec les trois axes du repère sont les sommets d'un triangle isocèle.
Soit A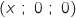 le point d'intersection de
le point d'intersection de  avec l'axe des abscisses, alors on a :
avec l'axe des abscisses, alors on a :
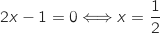 Donc A
Donc A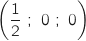 On détermine de même sans difficulté les coordonnées du point B d'intersection avec l'axe des ordonnées :
On détermine de même sans difficulté les coordonnées du point B d'intersection avec l'axe des ordonnées :
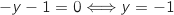 Donc B
Donc B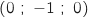 Enfin, on trouve les coordonnées du point C d'intersection avec l'axe des cotes :
Enfin, on trouve les coordonnées du point C d'intersection avec l'axe des cotes :
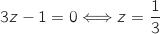 Donc C
Donc C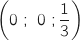 On calcule maintenant les longueurs des côtés du triangle ABC :
On calcule maintenant les longueurs des côtés du triangle ABC :
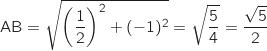
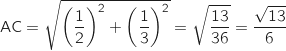
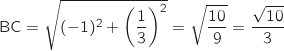 Ainsi les trois côtés du triangle sont de longueurs différentes donc ABC n'est pas isocèle.
L'affirmation est FAUSSE.
Ainsi les trois côtés du triangle sont de longueurs différentes donc ABC n'est pas isocèle.
L'affirmation est FAUSSE.
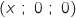 le point d'intersection de
le point d'intersection de  avec l'axe des abscisses, alors on a :
avec l'axe des abscisses, alors on a :
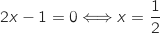 Donc A
Donc A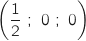 On détermine de même sans difficulté les coordonnées du point B d'intersection avec l'axe des ordonnées :
On détermine de même sans difficulté les coordonnées du point B d'intersection avec l'axe des ordonnées :
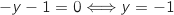 Donc B
Donc B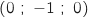 Enfin, on trouve les coordonnées du point C d'intersection avec l'axe des cotes :
Enfin, on trouve les coordonnées du point C d'intersection avec l'axe des cotes :
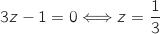 Donc C
Donc C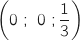 On calcule maintenant les longueurs des côtés du triangle ABC :
On calcule maintenant les longueurs des côtés du triangle ABC :
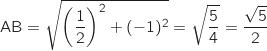
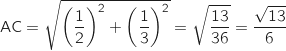
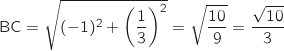 Ainsi les trois côtés du triangle sont de longueurs différentes donc ABC n'est pas isocèle.
L'affirmation est FAUSSE.
Ainsi les trois côtés du triangle sont de longueurs différentes donc ABC n'est pas isocèle.
L'affirmation est FAUSSE.
2. La droite
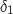 de représentation paramétrique
de représentation paramétrique
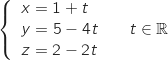
 .
.
La droite 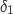 passe par le point de coordonnées
passe par le point de coordonnées 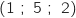 (on obtient ce point en prenant
(on obtient ce point en prenant 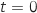 dans la représentation paramétrique).
or
dans la représentation paramétrique).
or 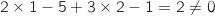 donc ce point n'appartient pas à
donc ce point n'appartient pas à  et la droite ne peut pas être incluse dans
et la droite ne peut pas être incluse dans  .
L'affirmation est FAUSSE.
.
L'affirmation est FAUSSE.
3. La droite 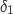 passe par le point de coordonnées
passe par le point de coordonnées 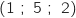 (on obtient ce point en prenant
(on obtient ce point en prenant 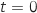 dans la représentation paramétrique).
or
dans la représentation paramétrique).
or 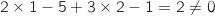 donc ce point n'appartient pas à
donc ce point n'appartient pas à  et la droite ne peut pas être incluse dans
et la droite ne peut pas être incluse dans  .
L'affirmation est FAUSSE.
.
L'affirmation est FAUSSE.
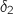 de représentation paramétrique
de représentation paramétrique
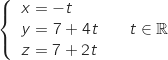
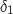 passant par le point S.
passant par le point S.
Par lecture sur les représentations paramétriques les droites 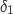 et
et 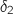 ont pour vecteurs
directeurs respectivement
ont pour vecteurs
directeurs respectivement 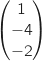 et
et 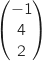 Ces deux vecteurs sont colinéaires donc
Ces deux vecteurs sont colinéaires donc 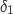 et
et 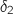 sont parallèles.
Il reste à vérifier que
sont parallèles.
Il reste à vérifier que 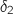 passe par S, pour cela on résout :
passe par S, pour cela on résout :
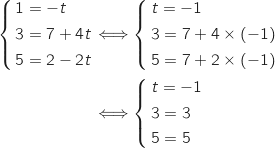 On aboutit à un système qui a une solution donc la droite
On aboutit à un système qui a une solution donc la droite 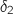 passe pas S.
L'affirmation est VRAIE.
passe pas S.
L'affirmation est VRAIE.
4. Le projeté orthogonal du point S sur le plan 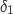 et
et 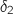 ont pour vecteurs
directeurs respectivement
ont pour vecteurs
directeurs respectivement 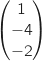 et
et 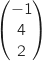 Ces deux vecteurs sont colinéaires donc
Ces deux vecteurs sont colinéaires donc 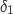 et
et 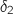 sont parallèles.
Il reste à vérifier que
sont parallèles.
Il reste à vérifier que 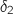 passe par S, pour cela on résout :
passe par S, pour cela on résout :
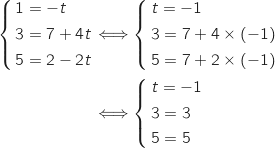 On aboutit à un système qui a une solution donc la droite
On aboutit à un système qui a une solution donc la droite 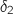 passe pas S.
L'affirmation est VRAIE.
passe pas S.
L'affirmation est VRAIE.
 a pour coordonnées
a pour coordonnées
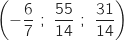
 est le point d'intersection du plan
est le point d'intersection du plan  avec la
droite orthogonale à
avec la
droite orthogonale à  passant par S.
passant par S.
On note H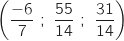 .
On remarque déjà que le point H appartient au plan
.
On remarque déjà que le point H appartient au plan  car :
car :
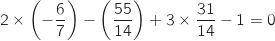 Il reste à vérifier que
Il reste à vérifier que 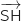 est orthogonal au plan
est orthogonal au plan  .
.
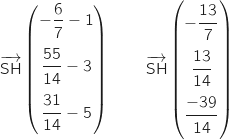 Un vecteur du plan
Un vecteur du plan  est
est 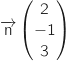 (lecture sur l'équation cartésienne).
On remarque que
(lecture sur l'équation cartésienne).
On remarque que 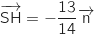 , donc
, donc 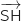 est orthogonal au plan
est orthogonal au plan  .
L'affirmation est VRAIE.
.
L'affirmation est VRAIE.
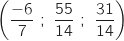 .
On remarque déjà que le point H appartient au plan
.
On remarque déjà que le point H appartient au plan  car :
car :
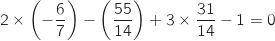 Il reste à vérifier que
Il reste à vérifier que 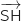 est orthogonal au plan
est orthogonal au plan  .
.
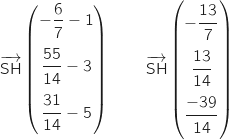 Un vecteur du plan
Un vecteur du plan  est
est 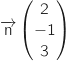 (lecture sur l'équation cartésienne).
On remarque que
(lecture sur l'équation cartésienne).
On remarque que 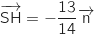 , donc
, donc 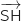 est orthogonal au plan
est orthogonal au plan  .
L'affirmation est VRAIE.
.
L'affirmation est VRAIE.
La dernière question de ce sujet nécessite l'utilisation de la formule de la distance d'un point à un plan. Cette formule ne figure plus dans les programmes.
