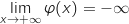Corrigé de l'exercice 1 du bac S de maths de juin 2012 aux Antilles
Cacher les corrigés
On note l'ensemble des nombres réels et on considère la fonction
l'ensemble des nombres réels et on considère la fonction  définie sur
définie sur  par
par
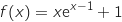
 sa courbe représentative dans un repère orthonormé
sa courbe représentative dans un repère orthonormé 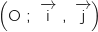 .
.
Partie A : étude de la fonction
1. Déterminer la limite de en
en  .
Que peut-on en déduire pour la courbe
.
Que peut-on en déduire pour la courbe  ?
?
On écrit 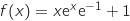 .
On sait par croissances comparées que
.
On sait par croissances comparées que 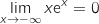 donc :
par produit
donc :
par produit 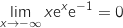 et par somme
et par somme 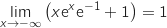 .
On en déduit que la courbe
.
On en déduit que la courbe  admet en
admet en  une asymptote « horizontale » d'équation
une asymptote « horizontale » d'équation 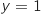 .
.
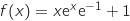 .
On sait par croissances comparées que
.
On sait par croissances comparées que 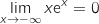 donc :
par produit
donc :
par produit 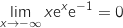 et par somme
et par somme 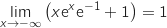 .
On en déduit que la courbe
.
On en déduit que la courbe  admet en
admet en  une asymptote « horizontale » d'équation
une asymptote « horizontale » d'équation 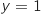 .
.
2. Déterminer la limite de
 en
en 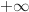 .
.
On a 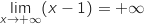 et par composition
et par composition 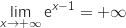 .
Par produit
.
Par produit 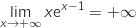 et en ajoutant 1 on obtient
et en ajoutant 1 on obtient 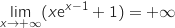 .
.
3. On admet que 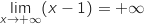 et par composition
et par composition 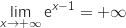 .
Par produit
.
Par produit 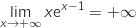 et en ajoutant 1 on obtient
et en ajoutant 1 on obtient 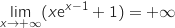 .
.
 est dérivable sur
est dérivable sur  , et on note
, et on note 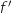 sa fonction dérivée.
Montrer que, pour tout réel
sa fonction dérivée.
Montrer que, pour tout réel 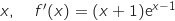 .
.
On peut écrire 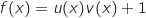 avec :
avec :
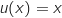
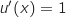
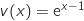
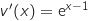 En utilisant la formule de dérivation d'un produit il vient :
En utilisant la formule de dérivation d'un produit il vient :
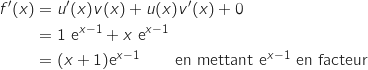
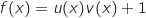 avec :
avec :
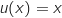
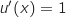
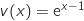
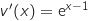 En utilisant la formule de dérivation d'un produit il vient :
En utilisant la formule de dérivation d'un produit il vient :
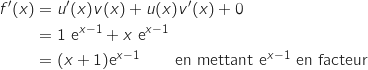
4. Etudier les variations de
 sur
sur  et dresser son tableau de variation sur
et dresser son tableau de variation sur  .
.
Pour tout  ,
, 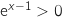 , donc le signe de
, donc le signe de  est le même que celui du binôme du premier degré
est le même que celui du binôme du premier degré 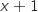 .
Ce binôme s'annule pour
.
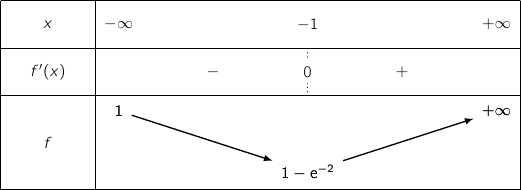
Ce binôme s'annule pour 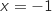 et on a le tableau de variation :
et on a le tableau de variation :
 ,
, 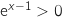 , donc le signe de
, donc le signe de  est le même que celui du binôme du premier degré
est le même que celui du binôme du premier degré 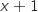 .
Ce binôme s'annule pour
.
Ce binôme s'annule pour 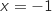 et on a le tableau de variation :
et on a le tableau de variation :

Partie B : recherche d'une tangente particulière
Soit un réel strictement positif. Le but de cette partie est de rechercher s'il existe une tangente à la courbe
un réel strictement positif. Le but de cette partie est de rechercher s'il existe une tangente à la courbe  au point d'abscisse
au point d'abscisse  , qui passe par l'origine du repère.
1. On appelle T
, qui passe par l'origine du repère.
1. On appelle T la tangente à
la tangente à  au point d'abscisse
au point d'abscisse  . Donner une équation de T
. Donner une équation de T .
.
L'équation réduite de la tangente au point d'abscisse  est :
est :
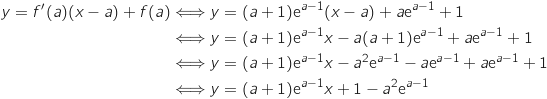
2. Démontrer qu'une tangente à  est :
est :
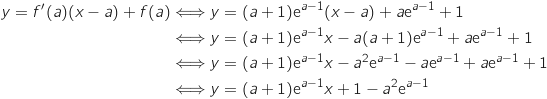
 en un point d'abscisse
en un point d'abscisse  strictement positive passe par l'origine du repère si et seulement si
strictement positive passe par l'origine du repère si et seulement si  vérifie l'égalité
vérifie l'égalité
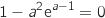
D'après la question précédente, l'ordonnée à l'origine de la droite 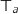 est
est 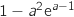 et donc cette droite passe par l'origine si et seulement si
et donc cette droite passe par l'origine si et seulement si 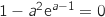 .
.
3. Dans cette question, toute trace de recherche même incomplète sera prise en compte dans l'évaluation.
Démontrer que 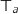 est
est 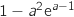 et donc cette droite passe par l'origine si et seulement si
et donc cette droite passe par l'origine si et seulement si 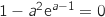 .
.
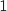 est l'unique solution sur l'intervalle
est l'unique solution sur l'intervalle 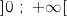 de l'équation
de l'équation
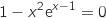
On vérifie déjà que 1 est bien solution de l'équation proposée : 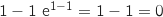 .
Il reste à montrer l'unicité. Pour cela on considère la fonction
.
Il reste à montrer l'unicité. Pour cela on considère la fonction  définie sur
définie sur  par :
par :
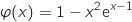
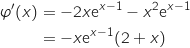 Pour
Pour 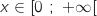 ,
, 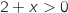 ,
, 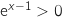 et
et 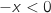 , donc
, donc 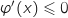 et s'annule uniquement pour
et s'annule uniquement pour 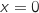 , ainsi la fonction
, ainsi la fonction  est strictement décroissante, plus précisément on a
le tableau de variation :
est strictement décroissante, plus précisément on a
le tableau de variation :
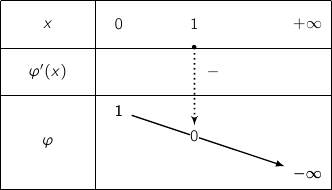
La fonction  est continue et strictement décroissante sur
est continue et strictement décroissante sur  avec :
avec :
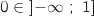 , d'après le théorème des valeurs intermédiaires on peut dire que l'équation
, d'après le théorème des valeurs intermédiaires on peut dire que l'équation 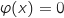 , c'est à dire
, c'est à dire 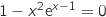 possède une unique solution
sur
possède une unique solution
sur  .
Donc 1 est l'unique solution sur
.
Donc 1 est l'unique solution sur 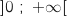 de l'équation
de l'équation 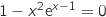 .
.
4. Donner alors une équation de la tangente recherchée.
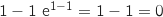 .
Il reste à montrer l'unicité. Pour cela on considère la fonction
.
Il reste à montrer l'unicité. Pour cela on considère la fonction  définie sur
définie sur  par :
par :
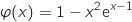
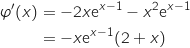 Pour
Pour 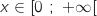 ,
, 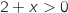 ,
, 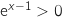 et
et 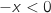 , donc
, donc 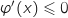 et s'annule uniquement pour
et s'annule uniquement pour 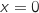 , ainsi la fonction
, ainsi la fonction  est strictement décroissante, plus précisément on a
le tableau de variation :
est strictement décroissante, plus précisément on a
le tableau de variation :

 est continue et strictement décroissante sur
est continue et strictement décroissante sur  avec :
avec :
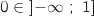 , d'après le théorème des valeurs intermédiaires on peut dire que l'équation
, d'après le théorème des valeurs intermédiaires on peut dire que l'équation 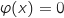 , c'est à dire
, c'est à dire 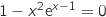 possède une unique solution
sur
possède une unique solution
sur  .
Donc 1 est l'unique solution sur
.
Donc 1 est l'unique solution sur 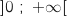 de l'équation
de l'équation 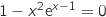 .
.
D'après ce qui précède, pour répondre à la question il faut prendre 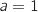 , ce qui donne l'équation
, ce qui donne l'équation 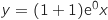 soit
soit 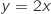 .
.
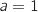 , ce qui donne l'équation
, ce qui donne l'équation 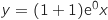 soit
soit 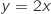 .
.
Partie C : calcul d'aire
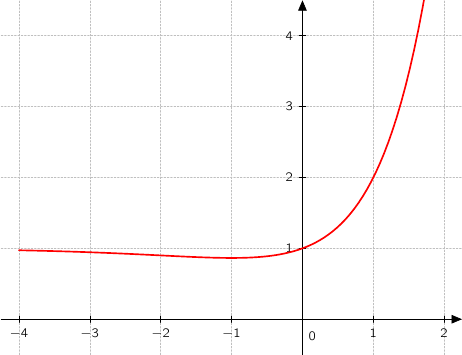
Le graphique donné ci-dessous représente la courbe de la fonction
de la fonction  dans un repère orthonormé
dans un repère orthonormé 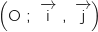 .
.
 d'équation
d'équation 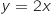 . On admet que la courbe
. On admet que la courbe  est au-dessus de la droite
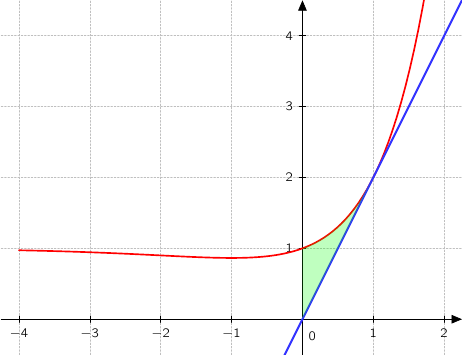
est au-dessus de la droite  . Hachurer le domaine
. Hachurer le domaine  limité par la courbe
limité par la courbe  la droite
la droite  , la droite d'équation
, la droite d'équation 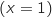 et l'axe des ordonnées.
et l'axe des ordonnées.
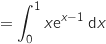 .
On admet que I
.
On admet que I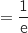 .
.
Dans le sujet original les élèves doivent calculer l'intégrale I en utilisant la méthode d'intégration par parties.
Cette méthode n'est plus dans les programmes à partir de la rentrée 2012.
3. En déduire la valeur exacte (en unités d'aire) de l'aire du domaine  .
.
Compte tenu de la position de  et
et  , l'aire considérée s'obtient en calculant :
, l'aire considérée s'obtient en calculant :
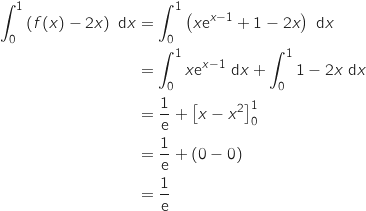 Donc l'aire de
Donc l'aire de  vaut
vaut  u.a.
u.a.
 et
et  , l'aire considérée s'obtient en calculant :
, l'aire considérée s'obtient en calculant :
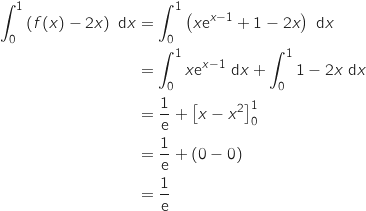 Donc l'aire de
Donc l'aire de  vaut
vaut  u.a.
u.a.