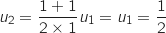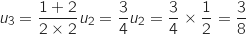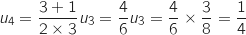Corrigé de l'exercice 3 de maths du bac S de juin 2012 aux Antilles
Cacher les corrigés
Soit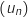 la suite définie pour tout entier naturel
la suite définie pour tout entier naturel  non nul par
non nul par
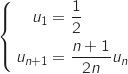
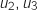 et
et 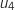 .
.
2.a. Démontrer que, pour tout entier naturel
 non nul,
non nul, 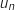 est strictement positif.
est strictement positif.
On montre cela par récurrence.
La propriété  à montrer pour tout entier naturel
à montrer pour tout entier naturel  non nul est :
non nul est :  : «
: « 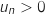 ».
Initialisation
On a
».
Initialisation
On a 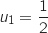 et
et 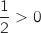 , donc
, donc 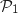 est vraie.
Hérédité
On suppose que la propriété est vraie à un rang
est vraie.
Hérédité
On suppose que la propriété est vraie à un rang 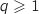 , c'est à dire que l'on a
, c'est à dire que l'on a 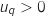 .
On cherche à montrer qu'avec cette hypothèse on a aussi
.
On cherche à montrer qu'avec cette hypothèse on a aussi 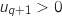 .
Par définition de la suite
.
Par définition de la suite 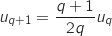 , comme
, comme 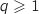 ,
, 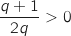 et comme par hypothèse
et comme par hypothèse 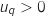 on en déduit que
on en déduit que 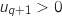 (c'est un produit de
deux quantités strictement positives), du coup
(c'est un produit de
deux quantités strictement positives), du coup  est vraie.
Ainsi la propriété
est vraie.
Ainsi la propriété  est vraie au rang 1 et elle est héréditaire, donc selon le principe de récurrence elle est vraie pour tout entier naturel
est vraie au rang 1 et elle est héréditaire, donc selon le principe de récurrence elle est vraie pour tout entier naturel  .
.
 à montrer pour tout entier naturel
à montrer pour tout entier naturel  non nul est :
non nul est :  : «
: « 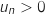 ».
Initialisation
On a
».
Initialisation
On a 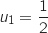 et
et 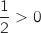 , donc
, donc 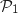 est vraie.
Hérédité
On suppose que la propriété est vraie à un rang
est vraie.
Hérédité
On suppose que la propriété est vraie à un rang 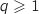 , c'est à dire que l'on a
, c'est à dire que l'on a 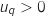 .
On cherche à montrer qu'avec cette hypothèse on a aussi
.
On cherche à montrer qu'avec cette hypothèse on a aussi 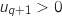 .
Par définition de la suite
.
Par définition de la suite 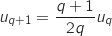 , comme
, comme 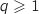 ,
, 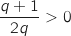 et comme par hypothèse
et comme par hypothèse 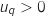 on en déduit que
on en déduit que 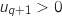 (c'est un produit de
deux quantités strictement positives), du coup
(c'est un produit de
deux quantités strictement positives), du coup  est vraie.
Ainsi la propriété
est vraie.
Ainsi la propriété  est vraie au rang 1 et elle est héréditaire, donc selon le principe de récurrence elle est vraie pour tout entier naturel
est vraie au rang 1 et elle est héréditaire, donc selon le principe de récurrence elle est vraie pour tout entier naturel  .
.
b. Démontrer que la suite
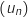 est décroissante.
est décroissante.
Comme 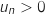 pour tout entier naturel
pour tout entier naturel  , on peut considérer le rapport :
, on peut considérer le rapport :
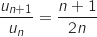 Pour tout
Pour tout  ,
, 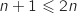 , donc
, donc 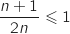 soit
soit 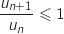 et comme
et comme 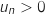 , cela prouve que
, cela prouve que 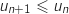 , donc que
, donc que  est décroissante.
est décroissante.
c. Que peut-on en déduire pour la suite 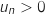 pour tout entier naturel
pour tout entier naturel  , on peut considérer le rapport :
, on peut considérer le rapport :
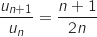 Pour tout
Pour tout  ,
, 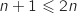 , donc
, donc 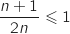 soit
soit 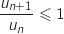 et comme
et comme 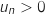 , cela prouve que
, cela prouve que 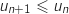 , donc que
, donc que  est décroissante.
est décroissante.
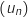 ?
?
La suite  est décroissante et minorée par 0 donc elle est convergente.
est décroissante et minorée par 0 donc elle est convergente.
3. Pour tout entier naturel  est décroissante et minorée par 0 donc elle est convergente.
est décroissante et minorée par 0 donc elle est convergente.
 non nul, on pose
non nul, on pose
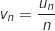
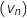 est géométrique.
On précisera sa raison et son premier terme
est géométrique.
On précisera sa raison et son premier terme 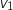 .
.
Pour tout entier  on a :
on a :
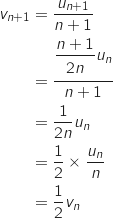 Donc la suite
Donc la suite  est une suite géométrique de raison
est une suite géométrique de raison  et de premier terme
et de premier terme 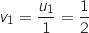 .
.
b. En déduire que, pour tout entier naturel  on a :
on a :
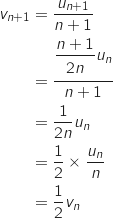 Donc la suite
Donc la suite  est une suite géométrique de raison
est une suite géométrique de raison  et de premier terme
et de premier terme 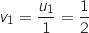 .
.
 non nul,
non nul,
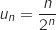
On a pour tout entier  :
:
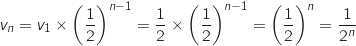 Comme
Comme 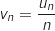 , on obtient
, on obtient 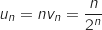 .
.
4. Soit la fonction  :
:
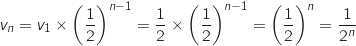 Comme
Comme 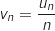 , on obtient
, on obtient 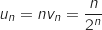 .
.
 définie sur l'intervalle
définie sur l'intervalle 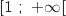 par
par 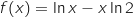 .
a. Déterminer la limite de
.
a. Déterminer la limite de  en
en 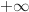 .
.
On a une forme indéterminée, pour lever l'indétermination on factorise par  .
Pour tout
.
Pour tout 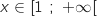 ,
, 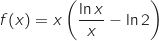 .
.
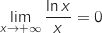 (croissances comparées)
par soustraction de
(croissances comparées)
par soustraction de 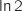 ,
, 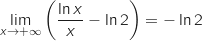 .
Pour finir, par produit,
.
Pour finir, par produit, 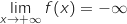 .
.
b. En déduire la limite de la suite  .
Pour tout
.
Pour tout 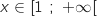 ,
, 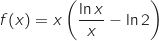 .
.
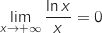 (croissances comparées)
par soustraction de
(croissances comparées)
par soustraction de 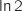 ,
, 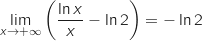 .
Pour finir, par produit,
.
Pour finir, par produit, 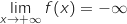 .
.
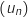 .
.
Pour tout entier  , on écrit :
, on écrit :
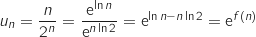 .
On a vu dans la question a. que
.
On a vu dans la question a. que 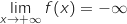 , donc en composant avec l'exponentielle on obtient
, donc en composant avec l'exponentielle on obtient
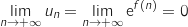 .
.
 , on écrit :
, on écrit :
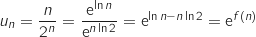 .
On a vu dans la question a. que
.
On a vu dans la question a. que 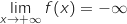 , donc en composant avec l'exponentielle on obtient
, donc en composant avec l'exponentielle on obtient
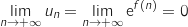 .
.