Corrigé de l'exercice 4 de maths du bac S de juin 2012 aux Antilles
Cacher les corrigés
Les cinq questions sont indépendantes. 1. Dans un lycée donné, on sait que 55 % des élèves sont des filles. On sait également que 35 % des filles et 30 % des garçons déjeunent à la cantine. On choisit, au hasard, un élève du lycée. Quelle est la probabilité que cet élève ne déjeune pas à la cantine ?
Dans ce lycée :
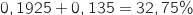 .
Donc il y a
.
Donc il y a 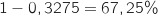 des élèves qui ne mangent pas à la cantine.
La probabilité demandée est donc
des élèves qui ne mangent pas à la cantine.
La probabilité demandée est donc 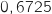 .
.
- la proportion de filles qui déjeunent à la cantine est :
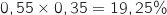 .
.
- la proportion de garçons qui déjeunent à la cantine est :
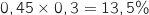 .
.
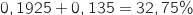 .
Donc il y a
.
Donc il y a 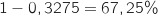 des élèves qui ne mangent pas à la cantine.
La probabilité demandée est donc
des élèves qui ne mangent pas à la cantine.
La probabilité demandée est donc 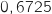 .
.
La question 2. du sujet original demande l'utilisation de notions de dénombrement qui ne sont plus au programme à
partir de la rentrée 2013.
3. Une variable aléatoire 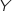 suit une loi binomiale de paramètres 20 et
suit une loi binomiale de paramètres 20 et  .
Calculer la probabilité que
.
Calculer la probabilité que 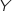 soit supérieure ou égale à 2. Donner une valeur approchée du résultat à
soit supérieure ou égale à 2. Donner une valeur approchée du résultat à 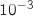 .
.
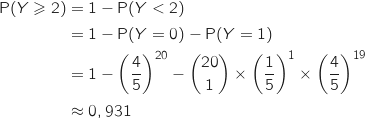
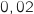 et que la probabilité que l'appareil présente au moins l'un des deux défauts est égale à
et que la probabilité que l'appareil présente au moins l'un des deux défauts est égale à 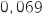 .
On choisit au hasard un des appareils.
Quelle est la probabilité que l'appareil présente le défaut F ?
.
On choisit au hasard un des appareils.
Quelle est la probabilité que l'appareil présente le défaut F ?
On sait que 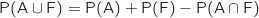 Comme A et F sont indépendants :
Comme A et F sont indépendants : 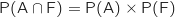 et en remplaçant les probabilités connues par leurs valeurs on obtient :
et en remplaçant les probabilités connues par leurs valeurs on obtient :
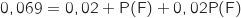 Il reste à résoudre cette équation dont l'inconnue est
Il reste à résoudre cette équation dont l'inconnue est 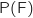 :
:
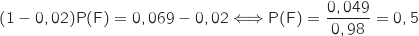
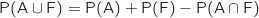 Comme A et F sont indépendants :
Comme A et F sont indépendants : 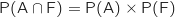 et en remplaçant les probabilités connues par leurs valeurs on obtient :
et en remplaçant les probabilités connues par leurs valeurs on obtient :
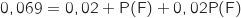 Il reste à résoudre cette équation dont l'inconnue est
Il reste à résoudre cette équation dont l'inconnue est 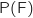 :
:
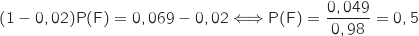
5. On considère l'algorithme :

 la variable aléatoire prenant la valeur C affichée.
Quelle loi suit la variable
la variable aléatoire prenant la valeur C affichée.
Quelle loi suit la variable  ? Préciser ses paramètres.
? Préciser ses paramètres.
On répère 9 fois le tirage au sort d'un nombre entre 1 et 7. A chaque fois on incrémente C lorsque la valeur tirée au sort vaut 6 ou 7, cela se produit donc avec une probabilité de  .
Donc
.
Donc  suit une loi binomiale
suit une loi binomiale 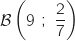 .
.
 .
Donc
.
Donc  suit une loi binomiale
suit une loi binomiale 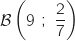 .
.
