Sujet et corrigé de l'exercice 1 du bac S de maths de juin 2013 aux Antilles
Cacher les corrigés
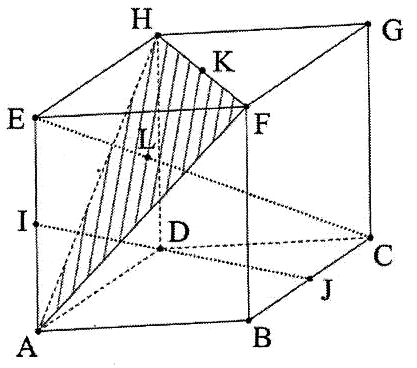
Description de la figure dans l'espace muni du repère orthonormé
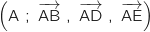 :
ABCDEFGH désigne un cube de côté 1.
On appelle
:
ABCDEFGH désigne un cube de côté 1.
On appelle  le plan (AFH).
Le point I est le milieu du segment [AE],
Le point J est le milieu du segment [BC],
Le point K est le milieu du segment [HF],
Le point L est le point d'intersection de la droite (EC) et du plan
le plan (AFH).
Le point I est le milieu du segment [AE],
Le point J est le milieu du segment [BC],
Le point K est le milieu du segment [HF],
Le point L est le point d'intersection de la droite (EC) et du plan  .
Ceci est un questionnaire à choix multiples (QCM). Pour chacune des questions, une seule
des quatre affirmations est exacte. Le candidat indiquera sur sa copie le numéro de la
question et la lettre correspondant à la réponse choisie. Aucune justification n'est demandée.
Une réponse exacte rapporte un point, une réponse fausse ou une absence de réponse ne rapporte aucun point.
1.
a. Les droites (IJ) et (EC) sont strictement parallèles.
b. Les droites (IJ) et (EC) sont non coplanaires.
c. Les droites (IJ) et (EC) sont sécantes.
d. Les droites (IJ) et (EC) sont confondues.
.
Ceci est un questionnaire à choix multiples (QCM). Pour chacune des questions, une seule
des quatre affirmations est exacte. Le candidat indiquera sur sa copie le numéro de la
question et la lettre correspondant à la réponse choisie. Aucune justification n'est demandée.
Une réponse exacte rapporte un point, une réponse fausse ou une absence de réponse ne rapporte aucun point.
1.
a. Les droites (IJ) et (EC) sont strictement parallèles.
b. Les droites (IJ) et (EC) sont non coplanaires.
c. Les droites (IJ) et (EC) sont sécantes.
d. Les droites (IJ) et (EC) sont confondues.
Les points E, I, J et C ne sont pas coplanaires car les droites (EI) et (JC) sont
portées par des arêtes non coplanaires du cube.
Du coup (IJ) et (EC) ne peuvent pas être coplanaires.
La bonne réponse est la réponse b.
2. a. Le produit scalaire
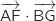 est égal à 0.
b. Le produit scalaire
est égal à 0.
b. Le produit scalaire 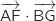 est égal à
est égal à 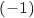 .
c. Le produit scalaire
.
c. Le produit scalaire 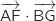 est égal à 1.
d. Le produit scalaire
est égal à 1.
d. Le produit scalaire 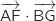 est égal à 2.
est égal à 2.
Dans le repère proposé on lit facilement les coordonnées des vecteurs :
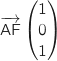 et
et
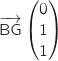
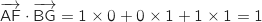 La bonne réponse est la réponse c.
La bonne réponse est la réponse c.
3. Dans le repère orthonormé 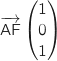 et
et
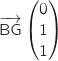
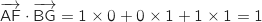 La bonne réponse est la réponse c.
La bonne réponse est la réponse c.
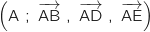 ,
a. le plan
,
a. le plan  a pour équation cartésienne :
a pour équation cartésienne : 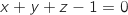 .
b. le plan
.
b. le plan  a pour équation cartésienne :
a pour équation cartésienne : 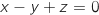 .
c. le plan
.
c. le plan  a pour équation cartésienne :
a pour équation cartésienne : 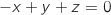 .
d. le plan
.
d. le plan  a pour équation cartésienne :
a pour équation cartésienne : 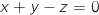 .
.
On peut déjà remarquer que  passe par l'origine du repère ce qui exclu la réponse a.
Les coordonnées de F sont
passe par l'origine du repère ce qui exclu la réponse a.
Les coordonnées de F sont 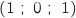 , en remplaçant ces coordonnées
dans les équations proposées on se rend compte que ça colle pas pour la proposition b.
Les coordonnées de H sont
, en remplaçant ces coordonnées
dans les équations proposées on se rend compte que ça colle pas pour la proposition b.
Les coordonnées de H sont 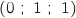 , en remplaçant ces coordonnées
dans l'équation proposée en c., ça ne colle pas, par contre en remplaçant dans d. oui !
Ainsi, les coordonnées des points A, H et F vérifient l'équation proposée en d.
La bonne réponse est la réponse d.
, en remplaçant ces coordonnées
dans l'équation proposée en c., ça ne colle pas, par contre en remplaçant dans d. oui !
Ainsi, les coordonnées des points A, H et F vérifient l'équation proposée en d.
La bonne réponse est la réponse d.
4.
a.  passe par l'origine du repère ce qui exclu la réponse a.
Les coordonnées de F sont
passe par l'origine du repère ce qui exclu la réponse a.
Les coordonnées de F sont 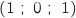 , en remplaçant ces coordonnées
dans les équations proposées on se rend compte que ça colle pas pour la proposition b.
Les coordonnées de H sont
, en remplaçant ces coordonnées
dans les équations proposées on se rend compte que ça colle pas pour la proposition b.
Les coordonnées de H sont 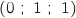 , en remplaçant ces coordonnées
dans l'équation proposée en c., ça ne colle pas, par contre en remplaçant dans d. oui !
Ainsi, les coordonnées des points A, H et F vérifient l'équation proposée en d.
La bonne réponse est la réponse d.
, en remplaçant ces coordonnées
dans l'équation proposée en c., ça ne colle pas, par contre en remplaçant dans d. oui !
Ainsi, les coordonnées des points A, H et F vérifient l'équation proposée en d.
La bonne réponse est la réponse d.
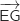 est un vecteur normal au plan
est un vecteur normal au plan  .
b.
.
b. 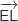 est un vecteur normal au plan
est un vecteur normal au plan  .
c.
.
c. 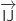 est un vecteur normal au plan
est un vecteur normal au plan  .
d.
.
d. 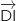 est un vecteur normal au plan
est un vecteur normal au plan  .
.
Par lecture sur l'équation cartésienne de  , un vecteur normal à ce plan
est
, un vecteur normal à ce plan
est 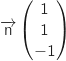 .
.
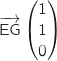 n'est pas colinéaire à
n'est pas colinéaire à  ,
ce qui exclu la réponse a.
Le vecteur
,
ce qui exclu la réponse a.
Le vecteur 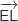 est colinéaire à
est colinéaire à 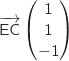 .
Ainsi
.
Ainsi 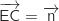 et donc
et donc 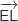 est un
vecteur normal de
est un
vecteur normal de  .
La bonne réponse est la réponse b.
Pour les coordonnées de
.
La bonne réponse est la réponse b.
Pour les coordonnées de 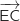 , si on n'est pas capable de faire la
lecture directe on peut les calculer à partir de E
, si on n'est pas capable de faire la
lecture directe on peut les calculer à partir de E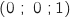 et C
et C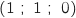
5.
a.  , un vecteur normal à ce plan
est
, un vecteur normal à ce plan
est 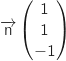 .
.
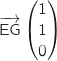 n'est pas colinéaire à
n'est pas colinéaire à  ,
ce qui exclu la réponse a.
Le vecteur
,
ce qui exclu la réponse a.
Le vecteur 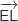 est colinéaire à
est colinéaire à 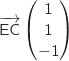 .
Ainsi
.
Ainsi 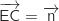 et donc
et donc 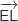 est un
vecteur normal de
est un
vecteur normal de  .
La bonne réponse est la réponse b.
Pour les coordonnées de
.
La bonne réponse est la réponse b.
Pour les coordonnées de 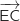 , si on n'est pas capable de faire la
lecture directe on peut les calculer à partir de E
, si on n'est pas capable de faire la
lecture directe on peut les calculer à partir de E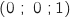 et C
et C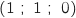
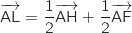 .
b.
.
b. 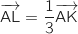 .
c.
.
c. 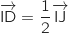 .
d.
.
d. 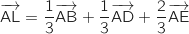 .
.
On peut déjà exclure la réponse c. car I, D et J ne sont pas alignés.
Du coup on ne peut pas échapper au calcul des coordonnées du point L.
Pour cela on a besoin d'une représentation paramétrique de (EC) : 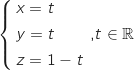 Pour trouver cette représentation on a utilisé le vecteur directeur
Pour trouver cette représentation on a utilisé le vecteur directeur 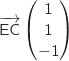 et
le point E
et
le point E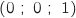 .
Comme L est à l'intersection de
.
Comme L est à l'intersection de  et (EC) on résout le système :
et (EC) on résout le système :
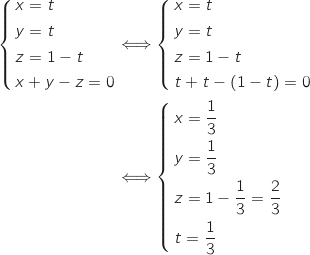 Du coup L
Du coup L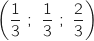 .
On remarque sans faire de calcul supplémentaire que la relation vectorielle donnée dans
la proposition d. donne pour L, dans le repère considéré, les coordonnées
que l'on vient de trouver.
La bonne réponse est la réponse d.
.
On remarque sans faire de calcul supplémentaire que la relation vectorielle donnée dans
la proposition d. donne pour L, dans le repère considéré, les coordonnées
que l'on vient de trouver.
La bonne réponse est la réponse d.
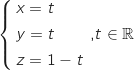 Pour trouver cette représentation on a utilisé le vecteur directeur
Pour trouver cette représentation on a utilisé le vecteur directeur 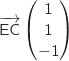 et
le point E
et
le point E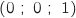 .
Comme L est à l'intersection de
.
Comme L est à l'intersection de  et (EC) on résout le système :
et (EC) on résout le système :
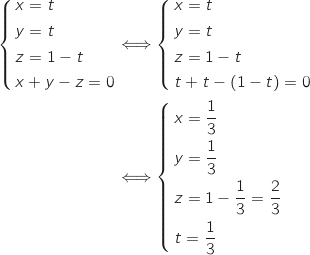 Du coup L
Du coup L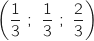 .
On remarque sans faire de calcul supplémentaire que la relation vectorielle donnée dans
la proposition d. donne pour L, dans le repère considéré, les coordonnées
que l'on vient de trouver.
La bonne réponse est la réponse d.
.
On remarque sans faire de calcul supplémentaire que la relation vectorielle donnée dans
la proposition d. donne pour L, dans le repère considéré, les coordonnées
que l'on vient de trouver.
La bonne réponse est la réponse d.
