Sujet et corrigé de l'exercice de spécialité du bac S de maths de juin 2013 aux Antilles
Cacher les corrigés
On définit les suite et
et  sur l'ensemble
sur l'ensemble 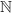 des entiers naturels par:
des entiers naturels par:
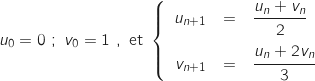
 et
et  .
.
1. Calculer
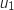 et
et 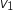 .
.
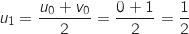
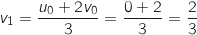

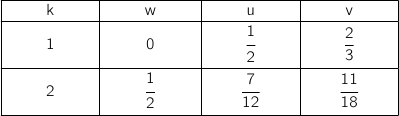
 . Recopier et compléter le tableau donné ci-dessous contenant l'état des variables au cours de l'exécution de l'algorithme.
. Recopier et compléter le tableau donné ci-dessous contenant l'état des variables au cours de l'exécution de l'algorithme.

-
 :
: 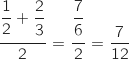
-
 :
: 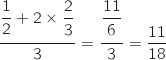
Les valeurs affichées sont les termes de rang N des suites  et
et  .
.
 et
et  .
.
3. Pour tout entier naturel
 on définit le vecteur colonne
on définit le vecteur colonne 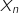 par
par 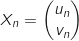 et la matrice A par
et la matrice A par 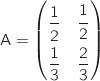 .
a. Vérifier que, pour tout entier naturel
.
a. Vérifier que, pour tout entier naturel  ,
, 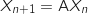 .
.
On calcule :
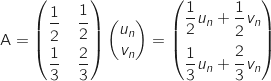 .
Avec :
.
Avec : 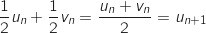 et :
et : 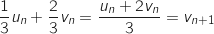 Donc on a bien
Donc on a bien 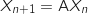 .
.
b. Démontrer par récurrence que 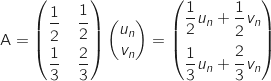 .
Avec :
.
Avec : 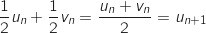 et :
et : 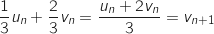 Donc on a bien
Donc on a bien 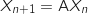 .
.
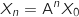 pour tout entier naturel
pour tout entier naturel  .
.
La propriété à montrer pour tout entier naturel  est :
est :
 : «
: « 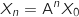 »
»
Initialisation :
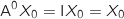 , donc
, donc 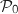 est vraie.
Hérédité
On suppose que la propriété est vraie à un rang
est vraie.
Hérédité
On suppose que la propriété est vraie à un rang  :
: 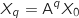 .
Montrons, qu'alors elle est vraie au rang
.
Montrons, qu'alors elle est vraie au rang 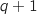 .
.
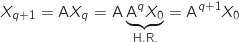 Donc
Donc  est vraie.
Ainsi
est vraie.
Ainsi  est vraie pour
est vraie pour 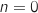 et est héréditaire donc la propriété est
vraie pour tout entier naturel
et est héréditaire donc la propriété est
vraie pour tout entier naturel  .
.
4. On définit les matrices P, P' et B par  est :
est :
 : «
: « 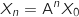 »
»
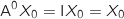 , donc
, donc 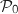 est vraie.
Hérédité
On suppose que la propriété est vraie à un rang
est vraie.
Hérédité
On suppose que la propriété est vraie à un rang  :
: 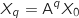 .
Montrons, qu'alors elle est vraie au rang
.
Montrons, qu'alors elle est vraie au rang 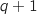 .
.
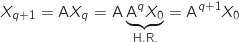 Donc
Donc  est vraie.
Ainsi
est vraie.
Ainsi  est vraie pour
est vraie pour  et est héréditaire donc la propriété est
vraie pour tout entier naturel
et est héréditaire donc la propriété est
vraie pour tout entier naturel  .
.
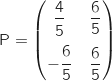 ,
, 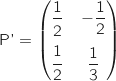 et
et 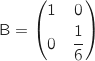 .
a. Calculer le produit PP'.
On admet que P'BP=A.
Démontrer par récurrence que pour tout entier naturel
.
a. Calculer le produit PP'.
On admet que P'BP=A.
Démontrer par récurrence que pour tout entier naturel  ,
, 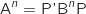 .
.
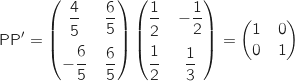 Cette fois la propriété à montrer pour tout entier naturel
Cette fois la propriété à montrer pour tout entier naturel  est :
est :
 : «
: « 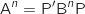 »
»
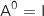 et
et 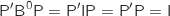 ,
donc on a
,
donc on a 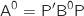 ce qui montre que
ce qui montre que 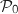 est vraie.
Hérédité
On suppose que
est vraie.
Hérédité
On suppose que 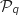 est vraie :
est vraie : 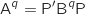 (hypothèse de récurrence).
Montrons qu'alors
(hypothèse de récurrence).
Montrons qu'alors  est vraie.
est vraie.
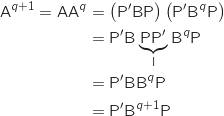 Ainsi,
Ainsi,  est vraie.
La propriété en question est initialisée au rang 0 ; elle est héréditaire, donc
elle est vraie pour tout entier naturel
est vraie.
La propriété en question est initialisée au rang 0 ; elle est héréditaire, donc
elle est vraie pour tout entier naturel  .
.
 ,
, 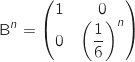 .
En déduire l'expression de la matrice
.
En déduire l'expression de la matrice 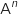 en fonction de
en fonction de  .
.
On calcule déjà :
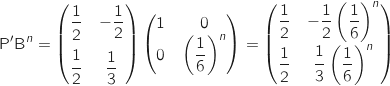 puis :
puis :
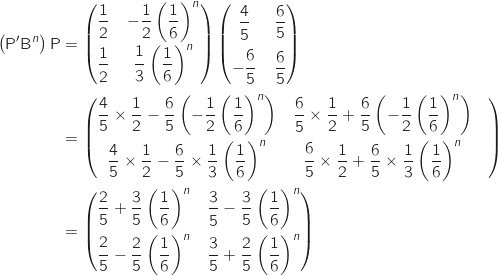
5.a. Montrer que 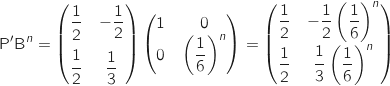 puis :
puis :
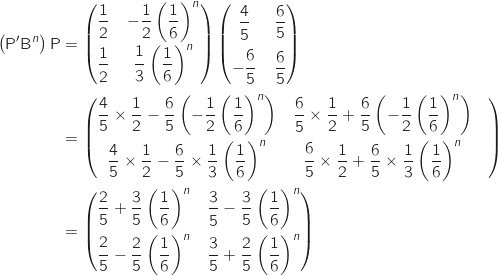
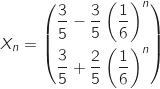 pour tout entier naturel
pour tout entier naturel  .
En déduire les expressions de
.
En déduire les expressions de 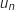 et
et 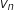 en fonction de
en fonction de  .
.
En utilisant l'expression de A trouvée à la question précédente on a :
trouvée à la question précédente on a :
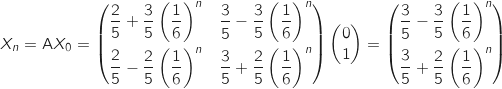
b. Déterminer alors les limites des suites  trouvée à la question précédente on a :
trouvée à la question précédente on a :
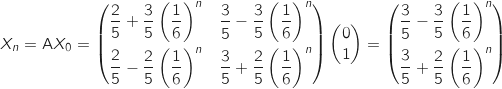
 et
et  .
.
Ainsi, 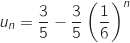 et
et
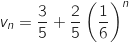 Comme
Comme 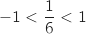 , on a
, on a 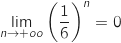 .
Du coup
.
Du coup 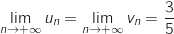 .
.
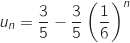 et
et
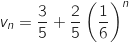 Comme
Comme 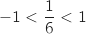 , on a
, on a 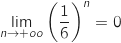 .
Du coup
.
Du coup 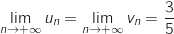 .
.
