Corrigé de l'exercice 2 du bac S de maths de juin 2012 en Asie
Cacher les corrigés
Le plan est muni d'un repère orthonormal direct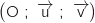 .
On considère le point A, d'affixe
.
On considère le point A, d'affixe 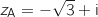 ,
le point A
,
le point A d'affixe
d'affixe 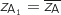 où
où 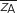 désigne le conjugué de
désigne le conjugué de 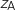 .
On note enfin B l'image du point A
.
On note enfin B l'image du point A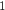 par la transformation complexe
par la transformation complexe 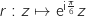 et
et 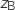 l'affixe du point B.
1.a. Ecrire le nombre complexe
l'affixe du point B.
1.a. Ecrire le nombre complexe 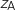 sous forme exponentielle, puis placer les points A et A
sous forme exponentielle, puis placer les points A et A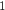 , dans le repère.
On prendra 2 cm comme unité graphique.
, dans le repère.
On prendra 2 cm comme unité graphique.
On a : 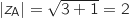 .
Donc on peut écrire
.
Donc on peut écrire 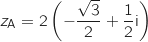 .
On cherche
.
On cherche 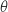 , tel que :
, tel que : 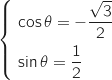 , on peut prendre
, on peut prendre 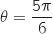 donc on a :
donc on a :
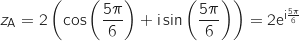
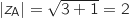 .
Donc on peut écrire
.
Donc on peut écrire 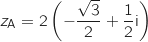 .
On cherche
.
On cherche 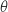 , tel que :
, tel que : 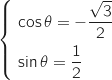 , on peut prendre
, on peut prendre 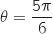 donc on a :
donc on a :
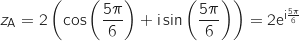
b. Vérifier que
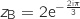 sous forme exponentielle, puis écrire le nombre complexe
sous forme exponentielle, puis écrire le nombre complexe  sous forme algébrique.
Placer alors le point B dans le même repère.
sous forme algébrique.
Placer alors le point B dans le même repère.
On a :
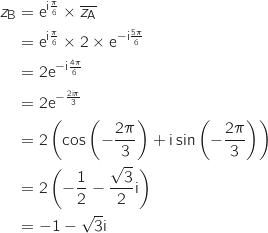
2. On considère le vecteur unitaire 

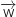 , tel que
, tel que 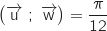 , et la droite
, et la droite  passant par O et de vecteur directeur
passant par O et de vecteur directeur 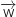 .
a. Démontrer que le triangle OAB est rectangle isocèle en O.
.
a. Démontrer que le triangle OAB est rectangle isocèle en O.
On calcule :
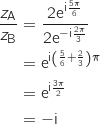 Du coup on a :
Du coup on a :
b. Tracer la droite 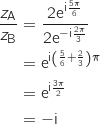 Du coup on a :
Du coup on a :
-
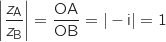 donc
donc 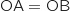 , ce qui prouve que OAB est isocèle en O.
, ce qui prouve que OAB est isocèle en O.
-
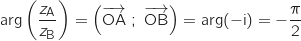 donc l'angle
donc l'angle 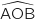 est droit ce qui prouve que OAB est rectangle en O.
est droit ce qui prouve que OAB est rectangle en O.
 , puis démontrer que
, puis démontrer que  est la bissectrice de l'angle
est la bissectrice de l'angle 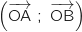 .
En déduire que les points A et B sont symétriques par rapport à la droite
.
En déduire que les points A et B sont symétriques par rapport à la droite  .
.
D'une part :
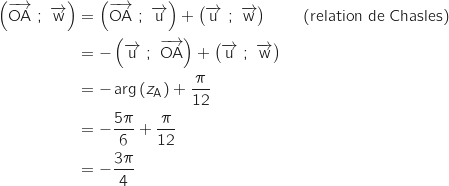 D'autre part :
D'autre part :
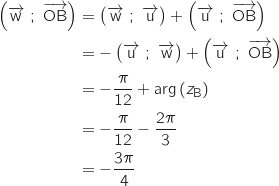 Du coup
Du coup 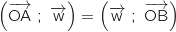 ce qui prouve que
ce qui prouve que  qui passe par O, est la bissectrice de
qui passe par O, est la bissectrice de 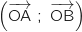 .
Le triangle OAB est isocèle en O donc la bissectrice issue de O est également la médiatrice du côté opposé [AB], il en résulte que A et B sont symétriques par rapport à
.
Le triangle OAB est isocèle en O donc la bissectrice issue de O est également la médiatrice du côté opposé [AB], il en résulte que A et B sont symétriques par rapport à  .
.
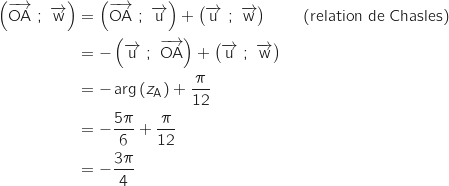 D'autre part :
D'autre part :
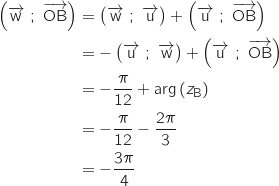 Du coup
Du coup 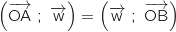 ce qui prouve que
ce qui prouve que  qui passe par O, est la bissectrice de
qui passe par O, est la bissectrice de 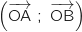 .
Le triangle OAB est isocèle en O donc la bissectrice issue de O est également la médiatrice du côté opposé [AB], il en résulte que A et B sont symétriques par rapport à
.
Le triangle OAB est isocèle en O donc la bissectrice issue de O est également la médiatrice du côté opposé [AB], il en résulte que A et B sont symétriques par rapport à  .
.
Dans le sujet d'origine l'exercice se termine par des questions qui font intervenir des transformations du plan. Le traitement par les nombres complexes de transformations du plan
ne fait plus partie des programmes à partir de la rentrée 2012.
