Corrigé de l'exercice 1 du bac S de maths de juin 2012 dans les centres étrangers
Cacher les corrigés
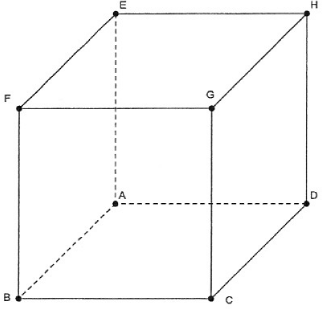
On considère un cube ABCDEFGH d'arête de longueur 1. On se place dans le repère orthonormal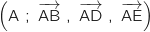 .
On considère les points I
.
On considère les points I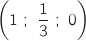 , J
, J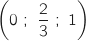 , K
, K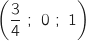 et L
et L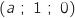 avec
avec
 un nombre réel appartenant à l'intervalle
un nombre réel appartenant à l'intervalle  .
.
Les parties A et B sont indépendantes
Partie A
1. Déterminer une représentation paramétrique de la droite (IJ).
Un vecteur directeur de la droite (IJ) est 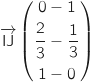 soit
soit
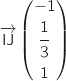 Donc une représentation paramétrique de la droite (IJ) est
Donc une représentation paramétrique de la droite (IJ) est 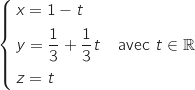
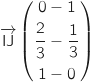 soit
soit
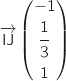 Donc une représentation paramétrique de la droite (IJ) est
Donc une représentation paramétrique de la droite (IJ) est 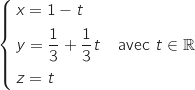
2. Démontrer que la droite (KL) a pour représentation paramétrique
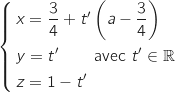
Un vecteur directeur de (KL) est le vecteur 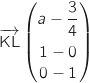 soit
soit
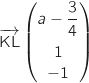 .
Donc une représentation paramétrique de (KL) s'écrit bien :
.
Donc une représentation paramétrique de (KL) s'écrit bien :
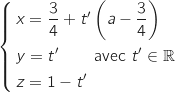
3. Démontrer que les droites (IJ) et (KL) sont sécantes si et seulement si 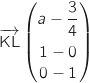 soit
soit
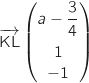 .
Donc une représentation paramétrique de (KL) s'écrit bien :
.
Donc une représentation paramétrique de (KL) s'écrit bien :
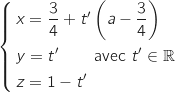
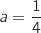 .
.
Les droites (IJ) et (KL) sont sécantes si et seulement si le système suivant admet un unique couple de solutions (pour les inconnues 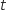 et
et 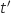 ) :
) :
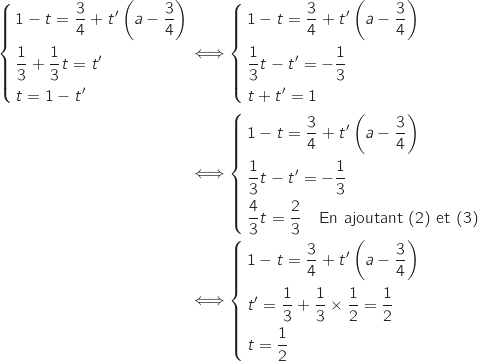 Le système ainsi obtenu admet un unique couple solution avec
Le système ainsi obtenu admet un unique couple solution avec 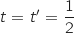 si et seulement on a l'égalité dans la première ligne du système donc si et seulement si
si et seulement on a l'égalité dans la première ligne du système donc si et seulement si
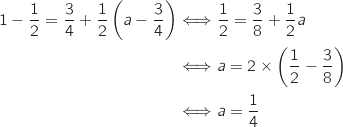
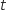 et
et 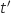 ) :
) :
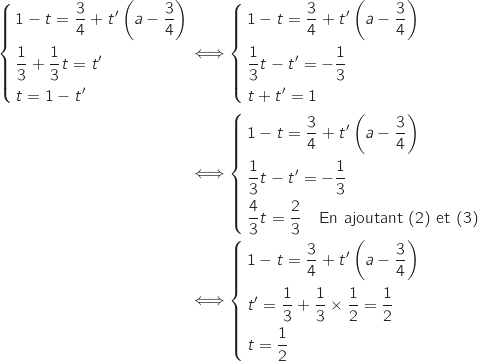 Le système ainsi obtenu admet un unique couple solution avec
Le système ainsi obtenu admet un unique couple solution avec 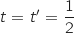 si et seulement on a l'égalité dans la première ligne du système donc si et seulement si
si et seulement on a l'égalité dans la première ligne du système donc si et seulement si
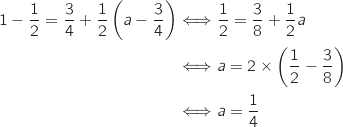
Partie B
Dans toute la suite de l'exercice, on pose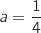 .
Le point L a donc pour coordonnées
.
Le point L a donc pour coordonnées 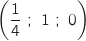 .
1. Démontrer que le quadrilatère IKJL est un parallélogramme.
.
1. Démontrer que le quadrilatère IKJL est un parallélogramme.
On a d'une part : 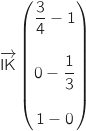 soit
soit 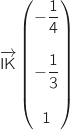 ,
et d'autre part :
,
et d'autre part : 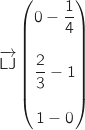 soit
soit 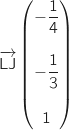 .
Du coup
.
Du coup 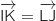 ce qui prouve que IKJL est un parallélogramme.
ce qui prouve que IKJL est un parallélogramme.
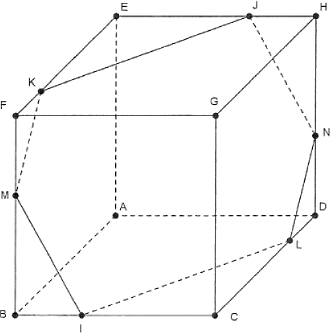
La figure ci-dessous fait apparaître l'intersection du plan (IJK) avec les faces du cube ABCDEFGH telle qu'elle a été obtenue à l'aide d'un logiciel de géométrie dynamique.
On désigne par M le point d'intersection du plan (IJK) et de la droite (BF) et par N le point d'intersection du plan (IJK) et de la droite (DH).
 soit
soit  ,
et d'autre part :
,
et d'autre part : 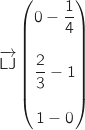 soit
soit  .
Du coup
.
Du coup 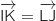 ce qui prouve que IKJL est un parallélogramme.
ce qui prouve que IKJL est un parallélogramme.
 de coordonnées
de coordonnées 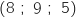 est un vecteur normal au plan (IJK).
est un vecteur normal au plan (IJK).
Les vecteurs 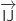 et
et 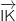 constituent un couple de vecteurs directeurs du plan (IJK).
Dans le repère orthonormal
constituent un couple de vecteurs directeurs du plan (IJK).
Dans le repère orthonormal 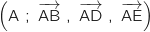 on a :
on a :
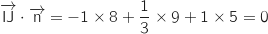
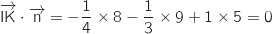 Ainsi, le vecteur
Ainsi, le vecteur  est orthogonal à deux vecteurs non colinéaires du plan (IJK), donc le vecteur
est orthogonal à deux vecteurs non colinéaires du plan (IJK), donc le vecteur  est normal au plan.
est normal au plan.
b. En déduire que le plan (IJK) a pour équation 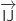 et
et 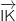 constituent un couple de vecteurs directeurs du plan (IJK).
Dans le repère orthonormal
constituent un couple de vecteurs directeurs du plan (IJK).
Dans le repère orthonormal 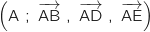 on a :
on a :
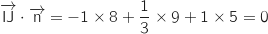
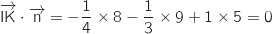 Ainsi, le vecteur
Ainsi, le vecteur  est orthogonal à deux vecteurs non colinéaires du plan (IJK), donc le vecteur
est orthogonal à deux vecteurs non colinéaires du plan (IJK), donc le vecteur  est normal au plan.
est normal au plan.
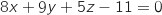 .
.
On sait que le vecteur 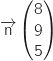 est un vecteur normal du plan donc une équation cartésienne du plan (IJK) est de la forme :
est un vecteur normal du plan donc une équation cartésienne du plan (IJK) est de la forme :
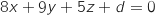
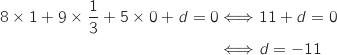 Donc une équation de (IJK) est bien
Donc une équation de (IJK) est bien 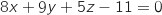 .
.
c. En déduire les coordonnées des points M et N.
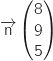 est un vecteur normal du plan donc une équation cartésienne du plan (IJK) est de la forme :
est un vecteur normal du plan donc une équation cartésienne du plan (IJK) est de la forme :
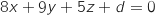
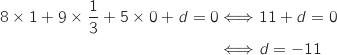 Donc une équation de (IJK) est bien
Donc une équation de (IJK) est bien 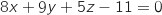 .
.
Coordonnées de M
M est le point d'intersection de la droite (BF) avec le plan (IJK).
Un représentation paramétrique de la droite (BF) est : 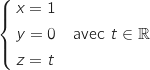 On résout le système :
On résout le système :
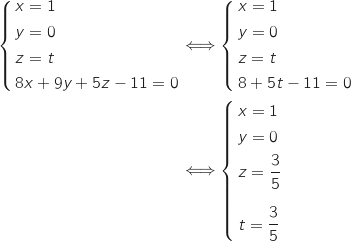 Donc M
Donc M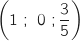 .
Coordonnées de N
N est le point d'intersection de la droite (DH) avec le plan (IJK).
Un représentation paramétrique de la droite (DH) est :
.
Coordonnées de N
N est le point d'intersection de la droite (DH) avec le plan (IJK).
Un représentation paramétrique de la droite (DH) est : 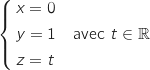 On résout le système :
On résout le système :
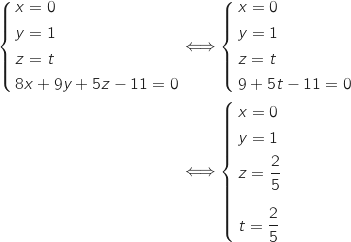 Donc N
Donc N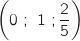 .
.
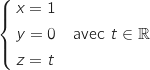 On résout le système :
On résout le système :
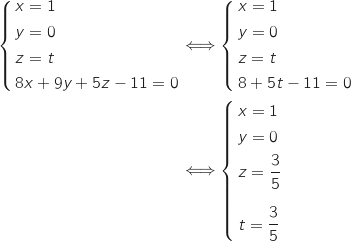 Donc M
Donc M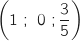 .
Coordonnées de N
N est le point d'intersection de la droite (DH) avec le plan (IJK).
Un représentation paramétrique de la droite (DH) est :
.
Coordonnées de N
N est le point d'intersection de la droite (DH) avec le plan (IJK).
Un représentation paramétrique de la droite (DH) est : 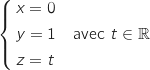 On résout le système :
On résout le système :
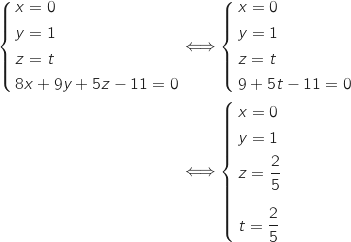 Donc N
Donc N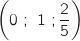 .
.
