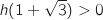Corrigé de l'exercice 3 du bac S de maths de juin 2012 dans les centres étrangers
Cacher les corrigés
On considère l'équation (E) d'inconnue réelle :
réelle : 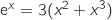 .
.
Partie A : Conjecture graphique
Le graphique ci-dessous donne la courbe représentative de la fonction exponentielle et celle de la fonction définie sur
définie sur  par :
par :
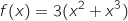
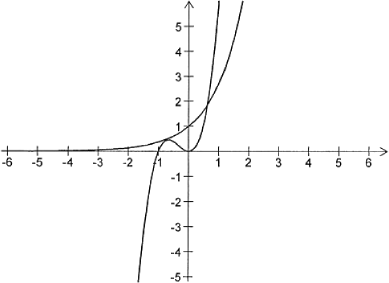
A l'aide du graphique ci-dessus, conjecturer le nombre de solutions de l'équation (E) et leur encadrement par deux entiers consécutifs.
On conjecture que l'équation possède deux solutions : une située dans l'intervalle 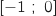 et l'autre dans
et l'autre dans  .
.
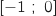 et l'autre dans
et l'autre dans  .
.
Partie B : Etude de la validité de la conjecture graphique
1.a. Etudier selon les valeurs de , le signe de
, le signe de 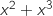 .
.
Pour tout réel  , on a
, on a 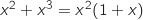 , donc le signe de l'expression est le même que celui de
, donc le signe de l'expression est le même que celui de 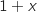 .
Cette dernière expression est un binôme du premier degré qui s'annule pour
.
Cette dernière expression est un binôme du premier degré qui s'annule pour 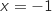 , ce qui donne le tableau de signes (on remarquera que
, ce qui donne le tableau de signes (on remarquera que 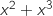 s'annule également pour
s'annule également pour 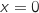 mais
sans changer de signe) :
mais
sans changer de signe) :

 , on a
, on a 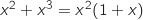 , donc le signe de l'expression est le même que celui de
, donc le signe de l'expression est le même que celui de 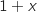 .
Cette dernière expression est un binôme du premier degré qui s'annule pour
.
Cette dernière expression est un binôme du premier degré qui s'annule pour 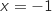 , ce qui donne le tableau de signes (on remarquera que
, ce qui donne le tableau de signes (on remarquera que 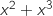 s'annule également pour
s'annule également pour 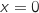 mais
sans changer de signe) :
mais
sans changer de signe) :

b. En déduire que l'équation (E) n'a pas de solution sur l'intervalle
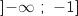 .
.
Sur 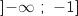 ,
, 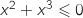 ,
or
,
or 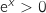 pour tout
pour tout  , donc on ne peut avoir, pour
, donc on ne peut avoir, pour 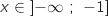 ,
, 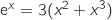 .
.
c. Vérifier que 0 n'est pas solution de l'équation (E).
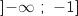 ,
, 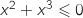 ,
or
,
or 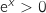 pour tout
pour tout  , donc on ne peut avoir, pour
, donc on ne peut avoir, pour 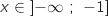 ,
, 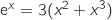 .
.
On a d'une part : 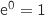 ,
et d'autre part :
,
et d'autre part : 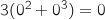 comme
comme  , 0 n'est pas solution de (E) !
, 0 n'est pas solution de (E) !
2. On considère la fonction 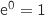 ,
et d'autre part :
,
et d'autre part : 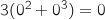 comme
comme 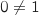 , 0 n'est pas solution de (E) !
, 0 n'est pas solution de (E) !
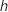 , définie pour tout nombre réel
, définie pour tout nombre réel  de
de 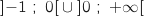 par :
par :
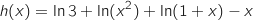
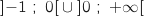 , l'équation (E) est équivalente à l'équation
, l'équation (E) est équivalente à l'équation 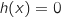 .
.
Sur l'intervalle considéré, d'après l'étude de signe de la question 1.a., les quantités qui interviennent dans les deux membres de l'équation sont strictement positives donc sous
réserve de travailler dans 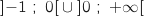 on a :
on a :
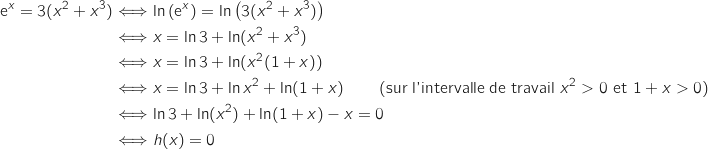
3.a. Montrer que, pour tout nombre réel 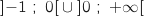 on a :
on a :
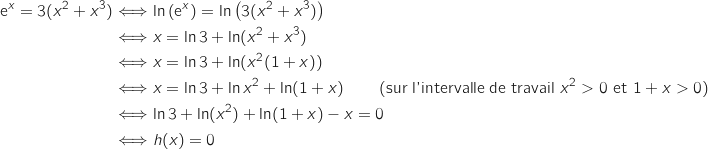
 appartenant à
appartenant à 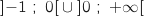 , on a :
, on a :
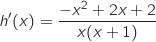
La fonction 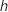 , considérée est dérivable sur l'intervalle précisé et on a :
, considérée est dérivable sur l'intervalle précisé et on a :
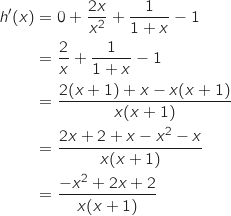
b. Déterminer les variations de 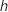 , considérée est dérivable sur l'intervalle précisé et on a :
, considérée est dérivable sur l'intervalle précisé et on a :
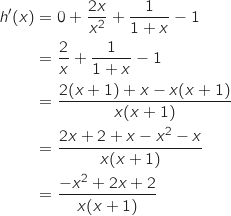
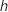 .
.
Pour tout réel  de
de 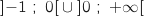 ,
, 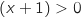 , donc le signe de la dérivée est le même que celui de
, donc le signe de la dérivée est le même que celui de 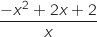 .
L'expression
.
L'expression 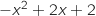 est un trinôme du second degré de discriminant :
est un trinôme du second degré de discriminant :
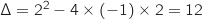 ,
Donc le trinôme possède deux racines qui sont :
,
Donc le trinôme possède deux racines qui sont :
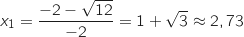 et
et 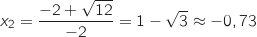 On en déduit le tableau de variations de
On en déduit le tableau de variations de 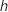 :
:
Détails :
Le trinôme est positif entre les racines 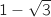 et
et 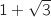 , mais pour
, mais pour 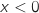 , le signe de
, le signe de 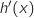 est opposé à cause du
est opposé à cause du  qui figure au dénominateur ce qui explique la ligne du signe de la dérivée.
En utilisant la calculette :
qui figure au dénominateur ce qui explique la ligne du signe de la dérivée.
En utilisant la calculette : 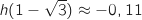 et
et 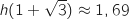 .
Limite à droite en 0
.
Limite à droite en 0
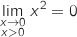 et par composition
et par composition 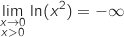 .
.
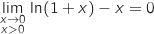 Par somme on a finalement :
Par somme on a finalement : 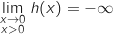 .
Limite en
.
Limite en  On a une forme indéterminée et pour tout
On a une forme indéterminée et pour tout 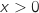 , on a :
, on a :
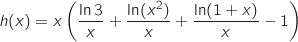
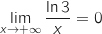
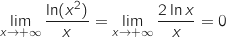 (croissance comparée).
(croissance comparée).
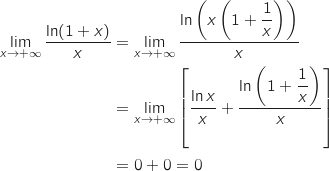 Par somme :
Par somme : 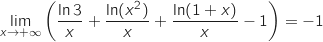 Finalement par produit
Finalement par produit 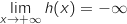 .
.
c. Déterminer le nombre de solutions de l'équation  de
de 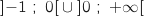 ,
, 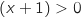 , donc le signe de la dérivée est le même que celui de
, donc le signe de la dérivée est le même que celui de 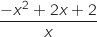 .
L'expression
.
L'expression 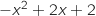 est un trinôme du second degré de discriminant :
est un trinôme du second degré de discriminant :
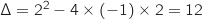 ,
Donc le trinôme possède deux racines qui sont :
,
Donc le trinôme possède deux racines qui sont :
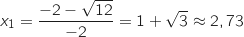 et
et 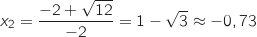 On en déduit le tableau de variations de
On en déduit le tableau de variations de 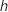 :
:

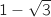 et
et 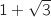 , mais pour
, mais pour 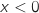 , le signe de
, le signe de 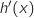 est opposé à cause du
est opposé à cause du  qui figure au dénominateur ce qui explique la ligne du signe de la dérivée.
En utilisant la calculette :
qui figure au dénominateur ce qui explique la ligne du signe de la dérivée.
En utilisant la calculette : 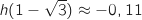 et
et 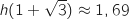 .
Limite à droite en 0
.
Limite à droite en 0
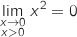 et par composition
et par composition 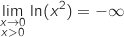 .
.
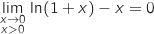 Par somme on a finalement :
Par somme on a finalement : 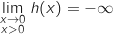 .
Limite en
.
Limite en  On a une forme indéterminée et pour tout
On a une forme indéterminée et pour tout 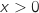 , on a :
, on a :
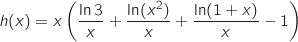
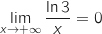
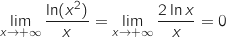 (croissance comparée).
(croissance comparée).
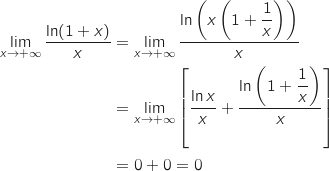 Par somme :
Par somme : 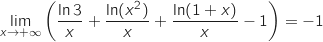 Finalement par produit
Finalement par produit 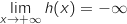 .
.
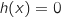 et donner une valeur arrondie au centième de chaque solution.
et donner une valeur arrondie au centième de chaque solution.
D'après l'étude de la question précédente, sur 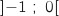 , l'équation
, l'équation 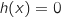 n'a pas de solution car sur cet intervalle le maximum de
n'a pas de solution car sur cet intervalle le maximum de 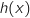 est strictement négatif.
En revanche sur l'intervalle
est strictement négatif.
En revanche sur l'intervalle 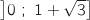 , la fonction
, la fonction 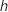 est continue et strictement croissante avec :
est continue et strictement croissante avec :
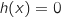 admet une unique solution
admet une unique solution 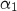 dans
dans 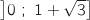 .
De la même façon, l'équation
.
De la même façon, l'équation 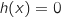 admet une deuxième solution
admet une deuxième solution 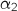 dans l'intervalle
dans l'intervalle 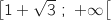 .
En utilisant la calculette on trouve :
.
En utilisant la calculette on trouve :
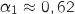 et
et 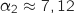 .
.
4. Conclure quant à la conjecture de la partie A.
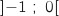 , l'équation
, l'équation 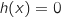 n'a pas de solution car sur cet intervalle le maximum de
n'a pas de solution car sur cet intervalle le maximum de 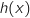 est strictement négatif.
En revanche sur l'intervalle
est strictement négatif.
En revanche sur l'intervalle 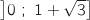 , la fonction
, la fonction 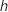 est continue et strictement croissante avec :
est continue et strictement croissante avec :
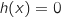 admet une unique solution
admet une unique solution 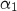 dans
dans 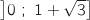 .
De la même façon, l'équation
.
De la même façon, l'équation 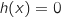 admet une deuxième solution
admet une deuxième solution 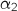 dans l'intervalle
dans l'intervalle 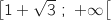 .
En utilisant la calculette on trouve :
.
En utilisant la calculette on trouve :
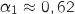 et
et 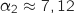 .
.
La conjecture est partiellement fausse.
- Les deux courbes ne se rencontrent pas sur
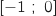 , bien qu'on en aie l'impression sur le graphique.
, bien qu'on en aie l'impression sur le graphique.
- La deuxième solution positive ne peut pas être lue sur le graphique présenté, car les deux courbes se coupent une deuxième fois en un point dont l'ordonnée est approximativement
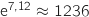 !
!