Corrigé de l'exercice 4 du bac S de maths de juin 2012 dans les centres étrangers
Cacher les corrigés
Les cinq questions sont indépendantes. Pour chaque question, une affirmation est proposée. Indiquer si elle est vraie ou fausse en justifiant la réponse. Une réponse non justifiée ne sera pas prise en compte. Toute trace de recherche sera valorisée. 1. On considère l'arbre de probabilités suivant :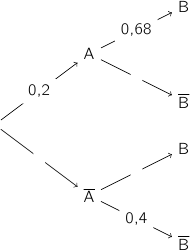
On peut déjà facilement compléter l'arbre avec les probabilités manquantes :
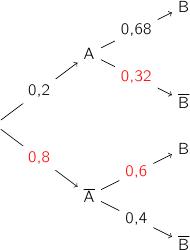
En utilisant la formule des probabilités conditionnelles on a :
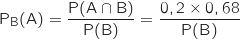 .
Pour calculer la probabilité de l'événement B on utilise la formule des probabilités totales avec le système complet d'événements
.
Pour calculer la probabilité de l'événement B on utilise la formule des probabilités totales avec le système complet d'événements 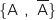 :
:
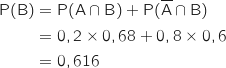 Du coup
Du coup 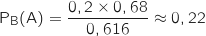 .
Donc l'affirmation est FAUSSE.
.
Donc l'affirmation est FAUSSE.

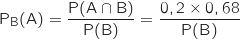 .
Pour calculer la probabilité de l'événement B on utilise la formule des probabilités totales avec le système complet d'événements
.
Pour calculer la probabilité de l'événement B on utilise la formule des probabilités totales avec le système complet d'événements 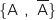 :
:
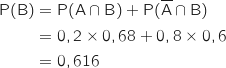 Du coup
Du coup 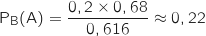 .
Donc l'affirmation est FAUSSE.
.
Donc l'affirmation est FAUSSE.
Dans le sujet original les questions 2. et 3. portent sur des notions qui ne figurent plus
au programme à partir de l'année scolaire 2012-2013.
4. Dans l'ensemble des nombres complexes, on considère l'équation (E) d'inconnue
 :
:
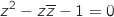
On pose 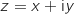 où
où  et
et 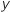 sont deux nombres réels.
sont deux nombres réels.
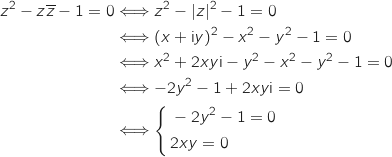 ce sytème n'a pas de solution car, par exemple,
ce sytème n'a pas de solution car, par exemple, 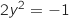 est impossible, donc l'équation initiale n'a pas de solution.
L'affirmation est FAUSSE.
est impossible, donc l'équation initiale n'a pas de solution.
L'affirmation est FAUSSE.
5. Dans le plan muni d'un repère orthonormal direct 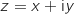 où
où  et
et 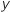 sont deux nombres réels.
sont deux nombres réels.
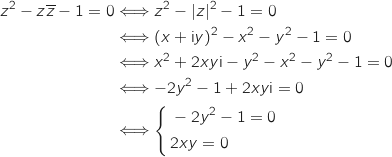 ce sytème n'a pas de solution car, par exemple,
ce sytème n'a pas de solution car, par exemple, 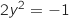 est impossible, donc l'équation initiale n'a pas de solution.
L'affirmation est FAUSSE.
est impossible, donc l'équation initiale n'a pas de solution.
L'affirmation est FAUSSE.
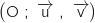 , on considère les points A, B et C
d'affixes respectives
, on considère les points A, B et C
d'affixes respectives 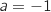 ,
, 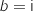 et
et 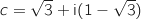 .
Affirmation : le triangle ABC possède un angle dont une mesure est égale à 60°.
.
Affirmation : le triangle ABC possède un angle dont une mesure est égale à 60°.
En faisant un petit dessin, on conjecture que l'angle en A mesure 60°, pour le vérifier on détermine 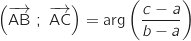 .
.
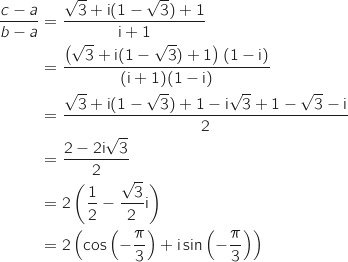 Donc
Donc 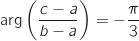 , et l'angle en A dans le triangle ABC mesure 60°.
L'affirmation est VRAIE.
, et l'angle en A dans le triangle ABC mesure 60°.
L'affirmation est VRAIE.
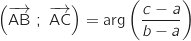 .
.
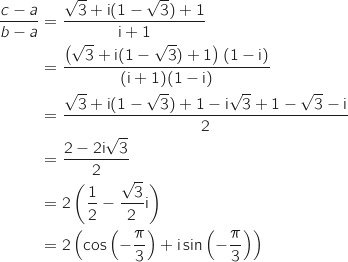 Donc
Donc 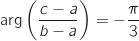 , et l'angle en A dans le triangle ABC mesure 60°.
L'affirmation est VRAIE.
, et l'angle en A dans le triangle ABC mesure 60°.
L'affirmation est VRAIE.
