Sujet et corrigé de l'exercice 1 du bac S de maths de juin 2013 dans les centres étrangers
Cacher les corrigés
Un industriel fabrique des vannes électroniques destinées à des circuits hydrauliques.
Partie A
La durée de vie d'une vanne, exprimée en heures, est une variable aléatoire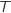
qui suit la loi exponentielle de paramètre 
.
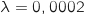1. Quelle est la durée de vie moyenne d'une vanne ?
La durée de vie moyenne d'une vanne correspond à l'espérance de 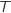. Or comme 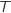suit une loi exponentielle on sait que :
.
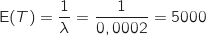Donc la durée de vie moyenne d'une vanne est de 5000 heures.
2. Calculer la probabilité, à 0,001 près, que la durée de vie d'une vanne soit supérieure à 6000 heures.
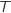. Or comme 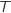suit une loi exponentielle on sait que :
.
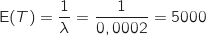Donc la durée de vie moyenne d'une vanne est de 5000 heures.
La fonction densité de probabilité associée à la loi exponentielle de paramètre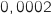 
est la
fonction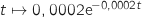 
, donc on a :
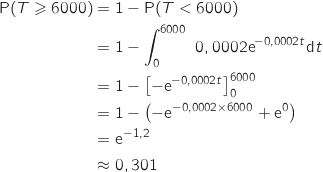
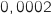est la
fonction 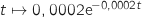, donc on a :
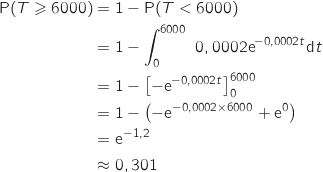
Partie B
Avec trois vannes identiques V
, V
, V
, on fabrique le circuit hydraulique ci-dessous.
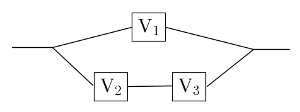
est en état de marche ou si V et V le sont simultanément.
On assimile à une expérience aléatoire le fait que chaque vanne est ou n'est pas pas en état de marche après 6000 heure. On note :
- F, l'événement : « la vanne V est en état de marche après 6000 heures » ;
- F, l'événement : « la vanne V est en état de marche après 6000 heures » ;
- F, l'événement : « la vanne V est en état de marche après 6000 heures » ;
- E l'événement : « le circuit est en état de marche après 6000 heures ».
, F, F sont deux à deux indépendants et ont chacun une probabilité égale à 0,3.
1. L'arbre probabiliste ci-dessous représente une partie de la situation.
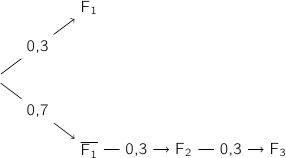
L'événement E correspond à la réunion des deux événements incompatibles :
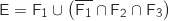ce qui donne :
.
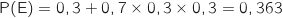3. Sachant que le circuit est en état de marche après 6000 heures, calculer la probabilité que la vanne V-
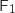(la vanne V fonctionne et peu importe
les vannes V et V)
-
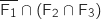(la
vanne V ne fonctionne pas et les vannes V et V fonctionnent)
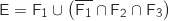ce qui donne :
.
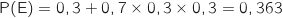soit en état de marche à ce moment là. Arrondir au millième.
On a :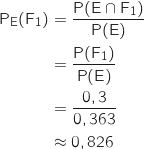 
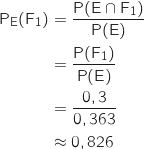
Partie C
L'industriel affirme que seulement 2 % des vannes qu'il fabrique sont défectueuses. On suppose que cette affirmation est vraie, et l'on note
la variable aléatoire égale à la fréquence de vannes
défectueuses dans un échantillon aléatoire de 400 vannes prises dans la production totale.
1. Déterminer l'intervalle I de fluctuation asymptotique au seuil de 95 % de la variable .
On utilise directement l'intervalle vu en cours :
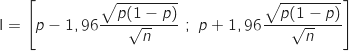
et 
.
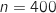On peut vérifier que les conditions habituelles d'utilisation sont vérifiées :
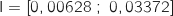
2. On choisit 400 vannes au hasard dans la production. On assimile ce choix à un tirage aléatoire
de 400 vannes, avec remise, dans la production.
Parmi ces 400 vannes, 10 sont défectueuses.
Au vu de ce résultat, peut-on remettre en cause, au seuil de 95 %, l'affirmation de l'industriel ?
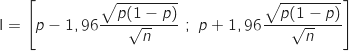
et .
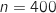On peut vérifier que les conditions habituelles d'utilisation sont vérifiées :
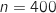- , donc
;
-
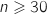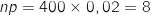, donc 
;
-
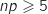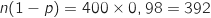, donc 
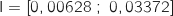
La proportion de vannes défectueuses observée dans l'échantillon ainsi réalisé est :
.
Or 
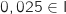, donc on ne peut pas remettre en cause l'affirmation de l'industriel.
.
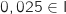Or , donc on ne peut pas remettre en cause l'affirmation de l'industriel.
Partie D
Dans cette partie, les probabilités calculées seront arrondies au millième. L'industriel commercialise ses vannes auprès de nombreux clients. La demande mensuelle est une variable aléatoire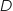
qui suit la loi normale d'espérance 
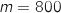et d'écart-type 
.
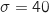1. Déterminer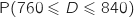 
.
En utilisant la calculette on obtient directement :
.
2. Déterminer .
.
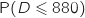Toujours avec la calculette on obtient :
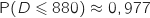
3. L'industriel pense que s'il constitue un stock mensuel de 880 vannes, il n'aura pas plus de 1 %
de chance d'être en rupture de stock. A-t-il raison ?
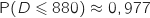
La probabilité pour qu'il soit en rupture de stock est :
.
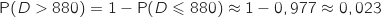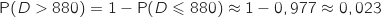Donc la probabilité qu'il soit en rupture de stock est d'environ 2,3 %, il a donc tort.
.
Donc la probabilité qu'il soit en rupture de stock est d'environ 2,3 %, il a donc tort.
