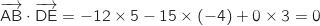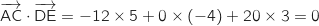Sujet et corrigé de l'exercice 2 du bac S de maths de juin 2013 dans les centres étrangers
Cacher les corrigés
Pour chaque affirmation, une affirmation est proposée. Indiquer si elle est vraie ou fausse, en justifiant la réponse. Une réponse non justifiée ne sera pas prise en compte.
Dans l'espace muni d'un repère orthonormé on considère :
- les points A
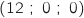 , B
, B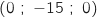 , C
, C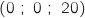 , D
, D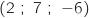 et E
et E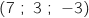 ;
;
- le plan
 d'équation cartésienne :
d'équation cartésienne : 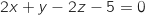 .
.
Affirmation 1
Une équation cartésienne du plan parallèle à et passant par le point A est :
et passant par le point A est :
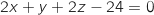
Par lecture sur l'équation de  , un vecteur normal à ce plan est
, un vecteur normal à ce plan est 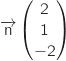 .
Le plan dont on propose une équation a pour vecteur normal
.
Le plan dont on propose une équation a pour vecteur normal 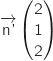 Les vecteur
Les vecteur  et
et 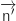 ne sont pas colinéaires, donc
les deux plans ne peuvent pas être parallèles.
L'affirmation est FAUSSE.
ne sont pas colinéaires, donc
les deux plans ne peuvent pas être parallèles.
L'affirmation est FAUSSE.
 , un vecteur normal à ce plan est
, un vecteur normal à ce plan est 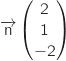 .
Le plan dont on propose une équation a pour vecteur normal
.
Le plan dont on propose une équation a pour vecteur normal 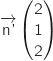 Les vecteur
Les vecteur  et
et 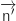 ne sont pas colinéaires, donc
les deux plans ne peuvent pas être parallèles.
L'affirmation est FAUSSE.
ne sont pas colinéaires, donc
les deux plans ne peuvent pas être parallèles.
L'affirmation est FAUSSE.
Affirmation 2
Une représentation paramétrique de la droite (AC) est :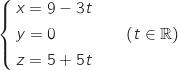
En prenant 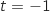 dans la représentation paramétrique on obtient :
dans la représentation paramétrique on obtient :
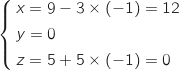 ce qui prouve que A appartient à la droite.
En prenant
ce qui prouve que A appartient à la droite.
En prenant 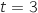 dans la représentation paramétrique on obtient :
dans la représentation paramétrique on obtient :
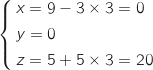 ce qui prouve que C appartient à la droite.
Ainsi la droite dont on donne la représentation paramétrique passe par A et C, donc elle
coïncide avec la droite (AC).
L'affirmation est VRAIE.
ce qui prouve que C appartient à la droite.
Ainsi la droite dont on donne la représentation paramétrique passe par A et C, donc elle
coïncide avec la droite (AC).
L'affirmation est VRAIE.
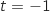 dans la représentation paramétrique on obtient :
dans la représentation paramétrique on obtient :
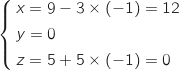 ce qui prouve que A appartient à la droite.
En prenant
ce qui prouve que A appartient à la droite.
En prenant 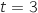 dans la représentation paramétrique on obtient :
dans la représentation paramétrique on obtient :
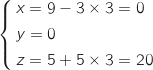 ce qui prouve que C appartient à la droite.
Ainsi la droite dont on donne la représentation paramétrique passe par A et C, donc elle
coïncide avec la droite (AC).
L'affirmation est VRAIE.
ce qui prouve que C appartient à la droite.
Ainsi la droite dont on donne la représentation paramétrique passe par A et C, donc elle
coïncide avec la droite (AC).
L'affirmation est VRAIE.
Affirmation 3
La droite (DE) et le plan ont au moins un point commun.
ont au moins un point commun.
Un vecteur directeur de (DE) est
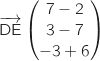 soit
soit
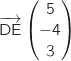 .
Un vecteur normal à
.
Un vecteur normal à  est
est 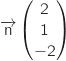 .
Le produit scalaire de ces deux vecteurs donne :
.
Le produit scalaire de ces deux vecteurs donne :
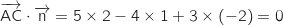 Cela signifie que la droite (DE) est parallèle au plan
Cela signifie que la droite (DE) est parallèle au plan  , il reste à savoir
si elle est incluse dans le plan ou si elle est strictement parallèle, pour cela on regarde, par
exemple, si le point D appartient au plan en testant si les coordonnées de
ce point vérifient l'équation cartésienne de
, il reste à savoir
si elle est incluse dans le plan ou si elle est strictement parallèle, pour cela on regarde, par
exemple, si le point D appartient au plan en testant si les coordonnées de
ce point vérifient l'équation cartésienne de  :
:
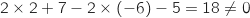 Donc
Donc 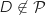 , du coup la droite est strictement parallèle au plan et n'a pas
de point commun avec lui.
L'affirmation est FAUSSE.
, du coup la droite est strictement parallèle au plan et n'a pas
de point commun avec lui.
L'affirmation est FAUSSE.
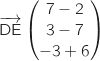 soit
soit
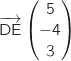 .
Un vecteur normal à
.
Un vecteur normal à  est
est 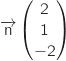 .
Le produit scalaire de ces deux vecteurs donne :
.
Le produit scalaire de ces deux vecteurs donne :
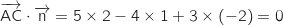 Cela signifie que la droite (DE) est parallèle au plan
Cela signifie que la droite (DE) est parallèle au plan  , il reste à savoir
si elle est incluse dans le plan ou si elle est strictement parallèle, pour cela on regarde, par
exemple, si le point D appartient au plan en testant si les coordonnées de
ce point vérifient l'équation cartésienne de
, il reste à savoir
si elle est incluse dans le plan ou si elle est strictement parallèle, pour cela on regarde, par
exemple, si le point D appartient au plan en testant si les coordonnées de
ce point vérifient l'équation cartésienne de  :
:
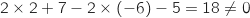 Donc
Donc 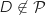 , du coup la droite est strictement parallèle au plan et n'a pas
de point commun avec lui.
L'affirmation est FAUSSE.
, du coup la droite est strictement parallèle au plan et n'a pas
de point commun avec lui.
L'affirmation est FAUSSE.
Affirmation 4
La droite (DE) est orthogonale au plan (ABC).
On commence par déterminer les coordonnées des vecteurs 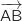 et
et
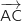 :
:
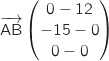 soit
soit
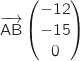
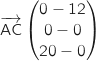 soit
soit
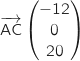 On remarque au passage que ces deux vecteurs ne sont pas colinéaires et que A, B et C définissent
bien un plan.
Pour savoir si (DE) est orthogonale à (ABC) on regarde si
On remarque au passage que ces deux vecteurs ne sont pas colinéaires et que A, B et C définissent
bien un plan.
Pour savoir si (DE) est orthogonale à (ABC) on regarde si 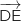 est
orthogonal à
est
orthogonal à 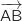 et
et 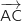 en faisant les
produits scalaires :
en faisant les
produits scalaires :
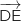 est orthogonal à deux vecteurs non colinéaires du plan, donc
la droite (DE) est orthogonale au plan (ABC).
L'affirmation est VRAIE.
est orthogonal à deux vecteurs non colinéaires du plan, donc
la droite (DE) est orthogonale au plan (ABC).
L'affirmation est VRAIE.
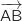 et
et
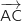 :
:
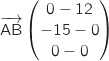 soit
soit
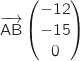
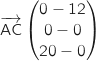 soit
soit
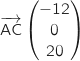 On remarque au passage que ces deux vecteurs ne sont pas colinéaires et que A, B et C définissent
bien un plan.
Pour savoir si (DE) est orthogonale à (ABC) on regarde si
On remarque au passage que ces deux vecteurs ne sont pas colinéaires et que A, B et C définissent
bien un plan.
Pour savoir si (DE) est orthogonale à (ABC) on regarde si 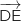 est
orthogonal à
est
orthogonal à 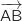 et
et 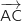 en faisant les
produits scalaires :
en faisant les
produits scalaires :
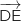 est orthogonal à deux vecteurs non colinéaires du plan, donc
la droite (DE) est orthogonale au plan (ABC).
L'affirmation est VRAIE.
est orthogonal à deux vecteurs non colinéaires du plan, donc
la droite (DE) est orthogonale au plan (ABC).
L'affirmation est VRAIE.