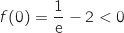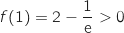Sujet et corrigé de l'exercice 3 du bac S de maths de juin 2013 dans les centres étrangers
Cacher les corrigés
On considère la fonction définie pour tout réel
définie pour tout réel  de l'intervalle
de l'intervalle  par :
par :
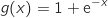
 de l'intervalle
de l'intervalle  ,
, 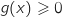 .
.
On note
 la courbe représentative de la fonction
la courbe représentative de la fonction  dans un repère orthogonal, et
dans un repère orthogonal, et  le domaine plan compris d'une part entre l'axe
des abscisses et la courbe
le domaine plan compris d'une part entre l'axe
des abscisses et la courbe  , d'autre part entre les droites d'équation
, d'autre part entre les droites d'équation 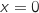 et
et  .
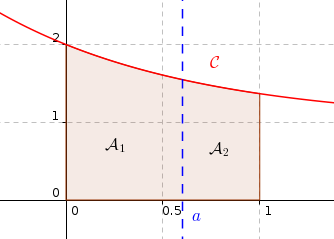
La courbe
.
La courbe  et le domaine
et le domaine  sont représentés ci-dessous.
sont représentés ci-dessous.
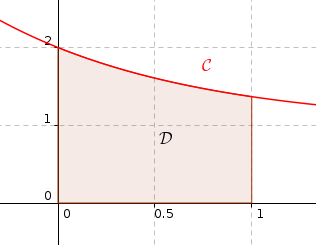
 en deux domaines de même aire,
d'abord par une droite parallèle à l'axe des ordonnées (partie A), puis par une droite parallèle à l'axe des abscisses (partie B).
en deux domaines de même aire,
d'abord par une droite parallèle à l'axe des ordonnées (partie A), puis par une droite parallèle à l'axe des abscisses (partie B).
Partie A
Soit un réel tel que
un réel tel que 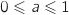 .
On note
.
On note 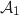 l'aire du domaine compris entre la courbe
l'aire du domaine compris entre la courbe  , l'axe
, l'axe 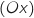 , les droites
d'équation
, les droites
d'équation 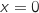 et
et 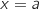 , puis
, puis 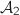 celle du domaine compris entre la courbe
celle du domaine compris entre la courbe  , l'axe
, l'axe
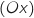 et les droites d'équation
et les droites d'équation 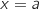 et
et  .
.
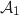 et
et 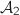 sont exprimées en unité d'aire.
sont exprimées en unité d'aire.
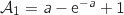 .
.
La fonction  étant continue et positive sur
étant continue et positive sur  , l'aire considérée s'exprime par l'intégrale :
, l'aire considérée s'exprime par l'intégrale :
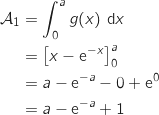
b. Exprimer  étant continue et positive sur
étant continue et positive sur  , l'aire considérée s'exprime par l'intégrale :
, l'aire considérée s'exprime par l'intégrale :
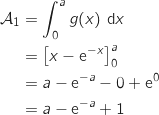
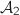 en fonction de
en fonction de  .
.
On a de même pour  :
:
2. Soit  :
:
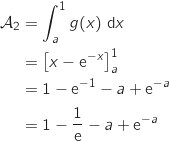
 la fonction définie pour tout réel
la fonction définie pour tout réel  de l'intervalle
de l'intervalle  par :
par :
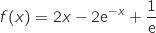
 sur l'intervalle
sur l'intervalle  . On précisera
les valeurs exactes de
. On précisera
les valeurs exactes de 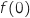 et
et 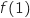 .
.
La fonction  est dérivable sur
est dérivable sur  et on a :
et on a :
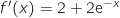 Il est évident que pour tout
Il est évident que pour tout 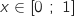 ,
, 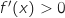 donc la fonction
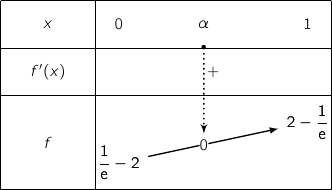
considérée est strictement croissante et on a le tableau de variations :
donc la fonction
considérée est strictement croissante et on a le tableau de variations :
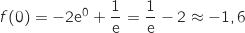
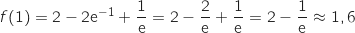
b. Démontrer que la fonction  est dérivable sur
est dérivable sur  et on a :
et on a :
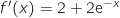 Il est évident que pour tout
Il est évident que pour tout 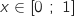 ,
, 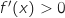 donc la fonction
considérée est strictement croissante et on a le tableau de variations :
donc la fonction
considérée est strictement croissante et on a le tableau de variations :

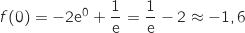
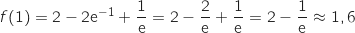
 s'annule une fois et une seule sur l'intervalle
s'annule une fois et une seule sur l'intervalle  en un réel
en un réel  .
Donner la valeur de
.
Donner la valeur de  arrondie au centième.
arrondie au centième.
La fonction  est continue et strictement croissante sur
est continue et strictement croissante sur  , avec :
, avec :
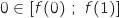 et d'après le théorème des valeurs intermédiaires
l'équation
et d'après le théorème des valeurs intermédiaires
l'équation 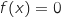 admet une unique solution dans l'intervalle
admet une unique solution dans l'intervalle  (l'unicité
étant assurée par la stricte croissance de
(l'unicité
étant assurée par la stricte croissance de  ).
En utilisant la calculette on trouve
).
En utilisant la calculette on trouve 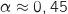 .
.
3. En utilisant les questions précédentes, déterminer une valeur approchée du réel  est continue et strictement croissante sur
est continue et strictement croissante sur  , avec :
, avec :
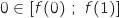 et d'après le théorème des valeurs intermédiaires
l'équation
et d'après le théorème des valeurs intermédiaires
l'équation 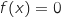 admet une unique solution dans l'intervalle
admet une unique solution dans l'intervalle  (l'unicité
étant assurée par la stricte croissance de
(l'unicité
étant assurée par la stricte croissance de  ).
En utilisant la calculette on trouve
).
En utilisant la calculette on trouve 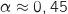 .
.
 pour lequel les aires
pour lequel les aires 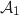 et
et 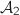 sont égales.
sont égales.
En utilisant les résultats de la question 1 on a :
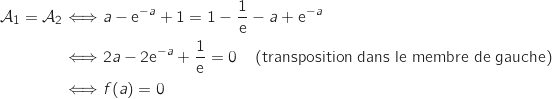 En utilisant la question 2. on en déduit qu'il existe une unique valeur de
En utilisant la question 2. on en déduit qu'il existe une unique valeur de  pour
laquelle
pour
laquelle 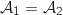 dont une valeur approchée est
dont une valeur approchée est 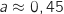 .
.
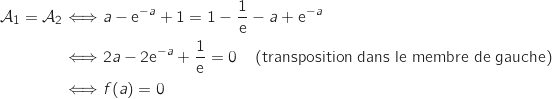 En utilisant la question 2. on en déduit qu'il existe une unique valeur de
En utilisant la question 2. on en déduit qu'il existe une unique valeur de  pour
laquelle
pour
laquelle 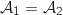 dont une valeur approchée est
dont une valeur approchée est 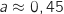 .
.
Partie B
Soit un réel positif.
Dans cette partie, on se propose de partager le domaine
un réel positif.
Dans cette partie, on se propose de partager le domaine  en deux domaines de même aire par la droite d'équation
en deux domaines de même aire par la droite d'équation 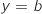 .
On admet qu'il existe un unique réel
.
On admet qu'il existe un unique réel  positif solution.
1. Justifier l'inégalité
positif solution.
1. Justifier l'inégalité 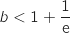 . On pourra utiliser un argument graphique.
. On pourra utiliser un argument graphique.
Un petit dessin :
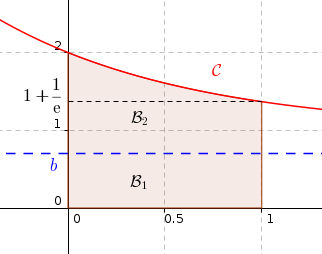
On cherche  tel que
tel que 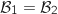 .
On peut facilement déterminer l'aire du domaine
.
On peut facilement déterminer l'aire du domaine  , en calculant, par exemple :
, en calculant, par exemple :
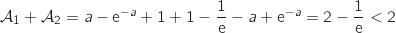 .
Donc
.
Donc 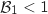 et compte-tenu de la situation (voir graphique), il n'est pas
possible d'avoir
et compte-tenu de la situation (voir graphique), il n'est pas
possible d'avoir 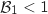 si
si 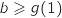 , donc
, donc 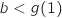 soit
soit 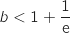 .
.
2. Déterminer la valeur exacte du réel 
 tel que
tel que 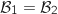 .
On peut facilement déterminer l'aire du domaine
.
On peut facilement déterminer l'aire du domaine  , en calculant, par exemple :
, en calculant, par exemple :
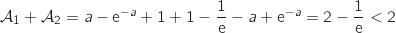 .
Donc
.
Donc 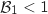 et compte-tenu de la situation (voir graphique), il n'est pas
possible d'avoir
et compte-tenu de la situation (voir graphique), il n'est pas
possible d'avoir 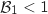 si
si 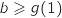 , donc
, donc 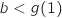 soit
soit 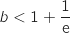 .
.
 .
.
Le domaine 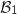 est un rectangle
dont un côté mesure 1 unité et dont l'aire doit être égale à la moitié de l'aire du domaine
est un rectangle
dont un côté mesure 1 unité et dont l'aire doit être égale à la moitié de l'aire du domaine  .
Donc
.
Donc  doit valoir la moitié de l'aire de
doit valoir la moitié de l'aire de  , ce qui donne :
, ce qui donne :
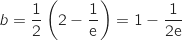 .
.
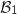 est un rectangle
dont un côté mesure 1 unité et dont l'aire doit être égale à la moitié de l'aire du domaine
est un rectangle
dont un côté mesure 1 unité et dont l'aire doit être égale à la moitié de l'aire du domaine  .
Donc
.
Donc  doit valoir la moitié de l'aire de
doit valoir la moitié de l'aire de  , ce qui donne :
, ce qui donne :
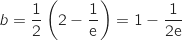 .
.