Sujet et corrigé de l'exercice 4 du bac S de maths de juin 2013 dans les centres étrangers
Cacher les corrigés
L'objet de cet exercice est l'étude de la suite définie par son premier terme
définie par son premier terme 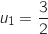 et
la relation de récurrence :
et
la relation de récurrence :
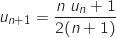
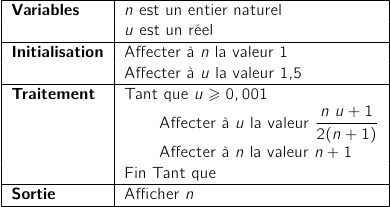
Partie A - Algorithmique et conjectures
Pour calculer et afficher le terme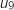 de la suite, un élève propose
l'algorithme ci-dessous dans lequel il a oublié de compléter deux lignes.
de la suite, un élève propose
l'algorithme ci-dessous dans lequel il a oublié de compléter deux lignes.
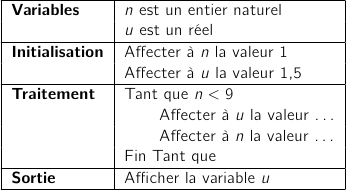
Il s'agit d'assurer qu'à chaque tour de boucle, le terme suivant de la suite soit calculé
en utilisant la relation de récurrence, ce qui donne :
Affecter à  la valeur
la valeur 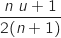 Affecter à
Affecter à  la valeur
la valeur 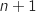
 la valeur
la valeur 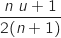 Affecter à
Affecter à  la valeur
la valeur 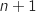
2. Comment faudrait-il modifier cet algorithme pour qu'il calcule et affiche tous les termes de la suite
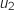 jusqu'à
jusqu'à 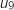 ?
?
Il faut placer l'instruction d'affichage dans la boucle, comme on veut
l'affichage de 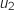 à
à 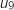 cette instruction doit figurer après l'affectation de
cette instruction doit figurer après l'affectation de  (si on place l'instruction avant on aura l'affichage des termes
de
(si on place l'instruction avant on aura l'affichage des termes
de 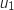 à
à 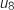 ). Cela donne l'algorithme :
). Cela donne l'algorithme :
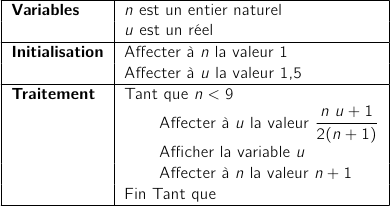
3. Avec cet algorithme modifié, on a obtenu les résultats suivants, arrondis au dix-millième :
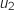 à
à 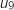 cette instruction doit figurer après l'affectation de
cette instruction doit figurer après l'affectation de  (si on place l'instruction avant on aura l'affichage des termes
de
(si on place l'instruction avant on aura l'affichage des termes
de 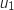 à
à 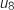 ). Cela donne l'algorithme :
). Cela donne l'algorithme :

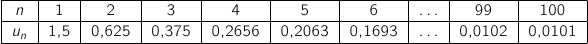 Au vu de ces résultats, conjecturer le sens de variation et la convergence de la suite
Au vu de ces résultats, conjecturer le sens de variation et la convergence de la suite  .
.
On peut conjecturer que la suite est décroissante et qu'elle converge vers 0.
Partie B - Etude mathématique
On définit une suite auxiliaire par :
pour tout entier
par :
pour tout entier  ,
, 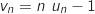 1. Monter que la suite
1. Monter que la suite  est géométrique ; préciser sa raison et son premier terme.
est géométrique ; préciser sa raison et son premier terme.
Pour tout entier  on a :
on a :
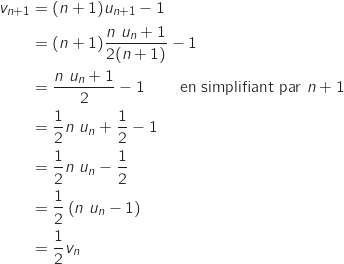 Cela prouve que la suite
Cela prouve que la suite  est une suite géométrique de raison
est une suite géométrique de raison  .
Son premier terme est
.
Son premier terme est 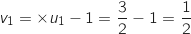 .
.
2. En déduire que pour tout entier  on a :
on a :
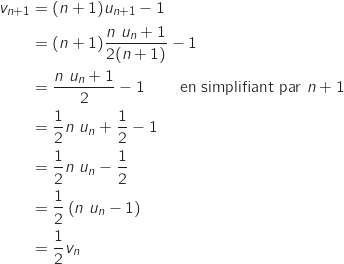 Cela prouve que la suite
Cela prouve que la suite  est une suite géométrique de raison
est une suite géométrique de raison  .
Son premier terme est
.
Son premier terme est 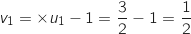 .
.
 , on a :
, on a : 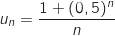 .
.
Puisque que  est géométrique, on peut exprimer
est géométrique, on peut exprimer 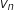 en fonction de
en fonction de  :
:
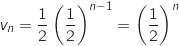 (on n'oublie pas que le premier terme est indicé 1)
On a de plus
(on n'oublie pas que le premier terme est indicé 1)
On a de plus 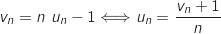 En remplaçant
En remplaçant 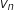 par son expression, il vient :
par son expression, il vient :
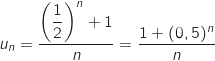
3. Déterminer la limite de la suite  est géométrique, on peut exprimer
est géométrique, on peut exprimer 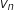 en fonction de
en fonction de  :
:
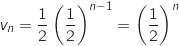 (on n'oublie pas que le premier terme est indicé 1)
On a de plus
(on n'oublie pas que le premier terme est indicé 1)
On a de plus 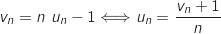 En remplaçant
En remplaçant 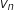 par son expression, il vient :
par son expression, il vient :
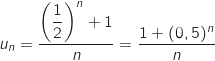
 .
.
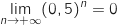 car
car 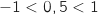 et par somme :
et par somme :
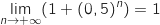 .
Donc
.
Donc 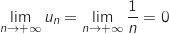
 , on a :
, on a :
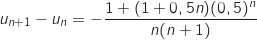
 .
.
Pour tout entier  on a :
on a :
 Tous les facteurs qui interviennent dans la fraction sont positifs, avec le signe
Tous les facteurs qui interviennent dans la fraction sont positifs, avec le signe  qui figure
devant le trait de fraction, on conclut que
qui figure
devant le trait de fraction, on conclut que 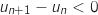 et donc que la suite
et donc que la suite  est
strictement décroissante.
est
strictement décroissante.
 on a :
on a :
 Tous les facteurs qui interviennent dans la fraction sont positifs, avec le signe
Tous les facteurs qui interviennent dans la fraction sont positifs, avec le signe  qui figure
devant le trait de fraction, on conclut que
qui figure
devant le trait de fraction, on conclut que 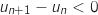 et donc que la suite
et donc que la suite  est
strictement décroissante.
est
strictement décroissante.
Partie C - Retour à l'algorithmique
En s'inspirant de la partie A, écrire un algorithme permettant de déterminer et d'afficher le plus petit entier tel que
tel que 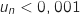 .
.