Sujet et corrigé de l'exercice 1 du bac S de maths de juin 2014 dans les centres étrangers
Cacher les corrigés
Cet exercice est un questionnaire à choix multiples comportant quatre questions indépendantes.
Pour chaque question, une seule des quatre affirmations proposées est exacte.
Indiquer la réponse exacte sans justification.
Question 1
Dans un hypermarché, 75 % des clients sont des femmes.
Une femme sur cinq achète un article au rayon bricolage, alors que sept hommes sur dix le font.
Une personne, choisie au hasard, a fait un achat au rayon bricolage.
La probabilité que cette personne soit une femme a pour valeur arrondie au millième :
| a. 0,750 | b. 0,150 | c. 0,462 | d. 0,700 |
Soit F l'événement : « Le client est une femme ».
Soit B l'événement : « La personne achète un article de bricolage ».
On peut représenter la situation par un arbre :
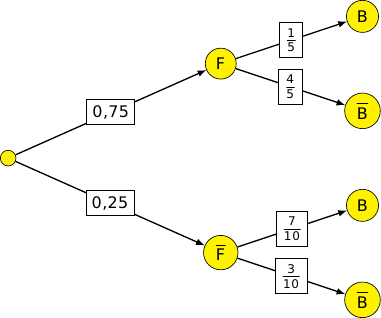
On calcule déjà la probabilité de l'événement B en utilisant la formule des probabilités totales :
Puis on calcule :
La bonne réponse est la réponse c.
Question 2
Dans cet hypermarché, un modèle d'ordinateur est en promotion.
Une étude statistique a permis d'établir que, chaque fois qu'un client s'intéresse à ce modèle, la probabilité qu'il l'achète est égale à 0,3.
On considère un échantillon aléatoire de dix clients qui se sont intéressés à ce modèle.
La probabilité qu'exactement trois d'entre eux aient acheté un ordinateur de ce modèle a pour valeur arrondie au millième :
| a. 0,900 | b. 0,092 | c. 0,002 | d. 0,267 |
La variable aléatoire qui compte le nombre de clients qui achètent l'ordinateur suit la loi binomiale de paramètres et , donc :
La bonne réponse est la réponse d.
Question 3
Cet hypermarché vend des téléviseurs dont la durée de vie, exprimée en année, peut être modélisée par une variable aléatoire réelle qui suit une loi exponentielle de paramètre .
La durée de vie moyenne d'un téléviseur est de huit ans, ce qui se traduit par : .
La probabilité qu'un téléviseur pris au hasard fonctionne encore au bout de six ans a pour valeur arrondie au millième :
| a. 0,750 | b. 0,250 | c. 0,472 | d. 0,528 |
En appelant la variable aléatoire qui donne la durée de vie du téléviseur, il s'agit de calculer :
La bonne réponse est la réponse c.
Question 4
Cet hypermarché vend des baguettes de pain dont la masse, exprimée en gramme, est une variable aléatoire réelle qui suit une loi normale de moyenne 200 g.
La probabilité que la masse d'une baguette soit comprise entre 184 g et 216 g est égale à 0,954.
La probabilité qu'une baguette prise au hasard ait une masse inférieure à 192 g a pour valeur arrondie au centième :
| a. 0,16 | b. 0,32 | c. 0,84 | d. 0,48 |
Soit la variable aléatoire qui suit la loi normale de moyenne 200 et d'écart-type inconnu.
Comme pour toute variable aléatoire qui suit une loi normale on a :
.
On remarque que et que et du coup :
, donc .
En utilisant la calculette on peut alors calculer :
La bonne réponse est la réponse a.
