Sujet et corrigé de l'exercice 2 du bac S de maths de juin 2014 dans les centres étrangers
Cacher les corrigés
On définit, pour tout entier naturel , les nombres complexes par :
On note le module du nombre complexe : .
Dans le plan muni d'un repère orthonormé direct d'origine O, on considère les points A d'affixes .
1.a. Calculer , et .
.
b. Placer les points A et A sur le graphique ci dessous :
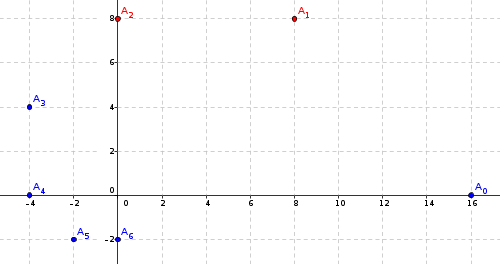
c. Ecrire le nombre complexe sous forme trigonométrique.
Donc :
d. Démontrer que le triangle OAA est isocèle rectangle en A.
OA
OA
AA
Donc OAA est bien isocèle en A.
De plus : et , donc OAA est également rectangle en A d'après la propriété de Pythagore.
2. Démontrer que la suite est géométrique, de raison .
La suite est-elle convergente ?
Interpréter géométriquement le résultat précédent.
Pour tout entier naturel on a :
Ce qui montre que la suite est une suite géométrique de raison .
Comme de plus , la suite converge vers 0.
Géométriquement les points A se rapprochent de l'origine du repère lorsque augmente.
On note L la longueur de la ligne brisée qui relie le point A au point A en passant successivement par les points A, A, A, etc.
Ainsi L
3.a. Démontrer que pour tout entier naturel : .
Pour tout entier naturel :
Comme , il vient :
b. Donner une expression de L en fonction de .
Du coup
où est une suite géométrique de raison .
Donc la somme des termes successifs est égale à :
c. Déterminer la limite éventuelle de la suite .
Comme , .
Du coup : .
Et par produit :
