Corrigé de l'exercice 2 du bac S de maths de mai 2012 au Liban
Cacher les corrigés
Dans cet exercice, pour chaque question, une affirmation est proposée. On demande d'indiquer sur la copie si elle est vraie ou fausse, en justifiant la réponse. Une réponse non justifiée ne sera pas prise en compte, mais toute trace de recherche sera valorisée. 1. Dans l'espace rapporté à un repère orthonormal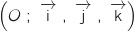
, on considère les droites 
et 
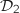de représenations paramétriques respectives:
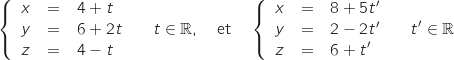
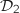et sont coplanaires.
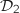Par lecture directe sur les représentations paramétriques de et , des vecteurs directeurs des deux droites en question sont respectivement 
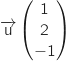et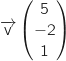 
.
On remarque que ces vecteurs ne sont pas colinéaires donc les droites ne sont pas parallèles.
On regarde maintenant si elles sont sécantes en cherchant leur point d'intersection éventuel. Pour cela on résout le système :
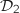Le système admet une unique solution, les droites et sont concourantes, donc elles sont coplanaires.
AFFIRMATION VRAIE.
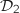et , des vecteurs directeurs des deux droites en question sont respectivemen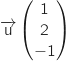t et .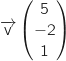
On remarque que ces vecteurs ne sont pas colinéaires donc les droites ne sont pas parallèles.
On regarde maintenant si elles sont sécantes en cherchant leur point d'intersection éventuel. Pour cela on résout le système :
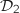Le système admet une unique solution, les droites et sont concourantes, donc elles sont coplanaires.
AFFIRMATION VRAIE.
2. Dans l'espace rapporté à un repère orthonormal
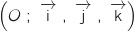, on considère les points
A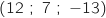
et B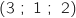
ainsi que le plan
d'équation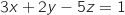 
.
Affirmation
Le point B est le projeté orthogonal du point A sur le plan .
On remarque déjà que le point B est dans le plan car les coordonnées de B vérifient l'équation du plan :
.
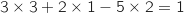Par lecture directe sur l'équation cartésienne, un vecteur normal du plan est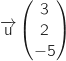 
.
Le vecteur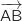 
a pour coordonnées : 
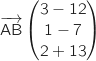soit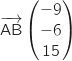 
.
On remarque que 
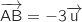, donc la droite (AB) est orthogonale au plan et comme B est dans ce plan, B est bien le projeté orthogonal de A sur .
AFFIRMATION VRAIE.
car les coordonnées de B vérifient l'équation du plan :
.
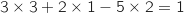Par lecture directe sur l'équation cartésienne, un vecteur normal du plan est .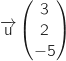
Le vecteur 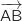a pour coordonnées : 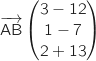soit .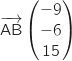
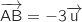On remarque que , donc la droite (AB) est orthogonale au plan et comme B est dans ce plan, B est bien le projeté orthogonal de A sur .
AFFIRMATION VRAIE.
Dans le sujet original la question 3. traite des suites adjacentes. Cette notion ne figure plus au
programme à compter de la rentrée 2012.
4. On considère la suite 
définie par son premier terme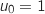 
et la relation de récurrence:
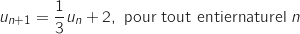
En calculant plusieurs termes de cette suite on conjecture que l'affirmation est vraie.
On va le démontrer par récurrence.
La propriété à montrer pour tout entier naturel 
est 
: « 
».
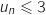Initialisation
On a 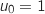, donc 
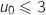et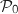 
est donc vraie.
Héredité
On suppose que la propriété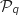 
est vraie à un rang 
, c'est à dire qu'on suppose que l'on a pour un entier naturel : 
.
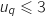On veut montrer qu'alors, 
est également vraie.
On part de l'hypothèse de récurrence et on a :
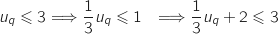Comme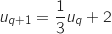 
, il vient 
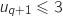, donc est vraie.
Ainsi la propriété est initialisée au rang 0, elle est héréditaire, donc selon le principe de récurrence elle est vraie pour tout entier naturel .
AFFIRMATION VRAIE.
est : « ».
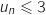Initialisation
On a 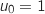, donc 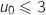et 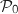est donc vraie.
Héredité
On suppose que la propriété 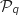est vraie à un rang , c'est à dire qu'on suppose que l'on a pour un entier naturel : .
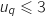On veut montrer qu'alors, est également vraie.
On part de l'hypothèse de récurrence et on a :
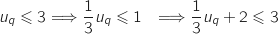Comme 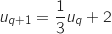, il vient 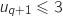, donc est vraie.
Ainsi la propriété est initialisée au rang 0, elle est héréditaire, donc selon le principe de récurrence elle est vraie pour tout entier naturel .
AFFIRMATION VRAIE.
