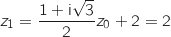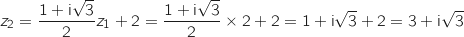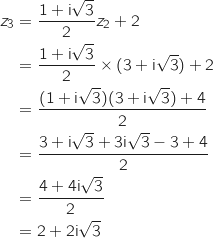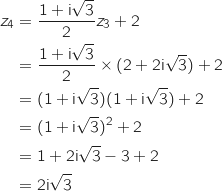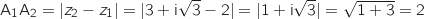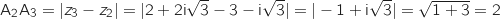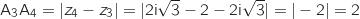Corrigé de l'exercice 4 du bac S de maths de mai 2012 au Liban
Cacher les corrigés
On se place dans le plan complexe muni d'un repère orthonormal direct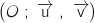 .
1. Un triangle
a. On considère les points A, B et C d'affixes respectives
.
1. Un triangle
a. On considère les points A, B et C d'affixes respectives 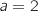 ,
, 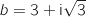 et
et 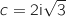 .
Déterminer une mesure de l'angle
.
Déterminer une mesure de l'angle  .
.
On sait qu'un argument de 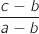 est aussi une mesure de l'angle
est aussi une mesure de l'angle 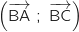 .
On a :
.
On a : 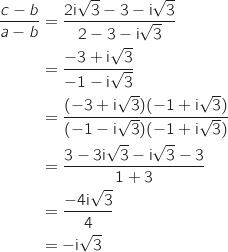 Donc
Donc 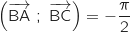 et l'angle
et l'angle 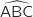 est droit.
est droit.
b. En déduire que l'affixe 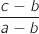 est aussi une mesure de l'angle
est aussi une mesure de l'angle 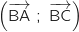 .
On a :
.
On a : 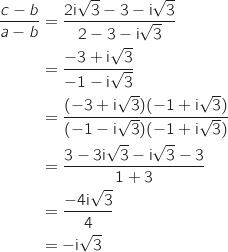 Donc
Donc 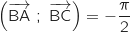 et l'angle
et l'angle 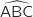 est droit.
est droit.
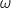 du centre
du centre 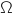 du cercle circonscrit au triangle ABC est
du cercle circonscrit au triangle ABC est 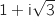 .
.
D'après la question précédente, le triangle ABC est rectangle en B, donc le centre 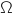 de son cercle circonscrit se trouve au milieu de l'hypoténuse [AC] et on a :
de son cercle circonscrit se trouve au milieu de l'hypoténuse [AC] et on a :
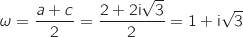 .
.
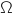 de son cercle circonscrit se trouve au milieu de l'hypoténuse [AC] et on a :
de son cercle circonscrit se trouve au milieu de l'hypoténuse [AC] et on a :
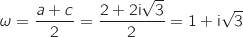 .
.
2. Une transformation du plan On note
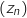 la suite de nombres complexes, de terme initiale
la suite de nombres complexes, de terme initiale 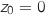 , et telle que:
, et telle que:
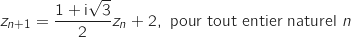
 , on note A
, on note A le point d'affixe
le point d'affixe 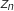 .
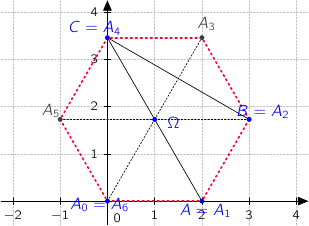
a. Montrer que les points A
.
a. Montrer que les points A , A
, A et A
et A ont pour affixes respectives:
ont pour affixes respectives:
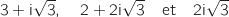
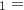 A, A
A, A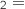 B et A
B et A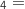 C.
C.
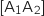 ,
, 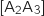 et
et 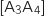 .
.
 , on a:
, on a:
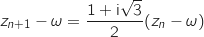
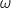 désigne le nombre complexe défini à la question 1.b.
désigne le nombre complexe défini à la question 1.b.
Pour tout entier naturel  , on a :
, on a :
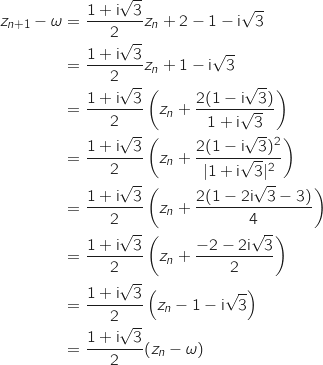
 , on a :
, on a :
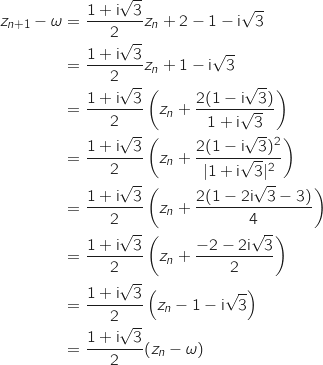
Dans le sujet original la question d. fait référence à la notion de rotation qui ne figure plus dans les programmes
à partir de la rentrée 2012.
e. En remarquant que 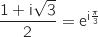 , justifier que, pour tout entier naturel
, justifier que, pour tout entier naturel  , on a:
, on a: 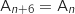 .
Déterminer l'affixe du point
.
Déterminer l'affixe du point 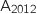 .
.
D'après ce qui précède on a la relation : 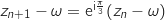 et pour tout entier naturel
et pour tout entier naturel  :
:
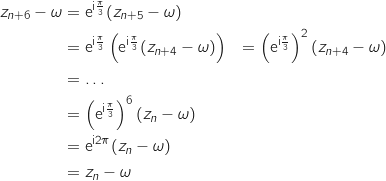 Donc
Donc 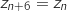 , c'est à dire que
, c'est à dire que 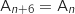 .
On effectue maintenant la division euclidienne de 2012 par 6 :
.
On effectue maintenant la division euclidienne de 2012 par 6 : 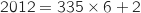 .
Du coup on a :
.
Du coup on a : 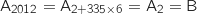 .
.
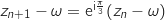 et pour tout entier naturel
et pour tout entier naturel  :
:
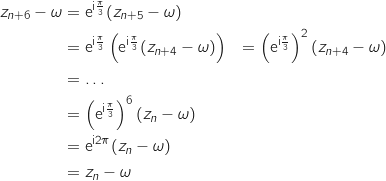 Donc
Donc 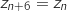 , c'est à dire que
, c'est à dire que 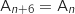 .
On effectue maintenant la division euclidienne de 2012 par 6 :
.
On effectue maintenant la division euclidienne de 2012 par 6 : 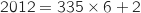 .
Du coup on a :
.
Du coup on a : 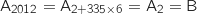 .
.