Sujet et corrigé de l'exercice 1 du bac S de maths de mai 2013 au Liban
Cacher les corrigés
Cet exercice est un questionnaire à choix multiples. Aucune justification n'est demandée. Pour chacune des questions, une seule des propositions est correcte. Chaque réponse correcte rapporte un point. Une réponse erronée ou une absence de réponse n'ôte pas de point. On notera sur la copie le numéro de la question, suivi de la lettre correspondant à la proposition choisie. L'espace est rapporté à un repère orthonormé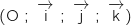 .
Les points A, B, C et D ont pour coordonnées respectives :
A
.
Les points A, B, C et D ont pour coordonnées respectives :
A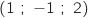 , B
, B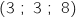 , C
, C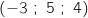 et D(1 ; 2 ; 3).
On note
et D(1 ; 2 ; 3).
On note  la droite ayant pour représentation paramétrique :
la droite ayant pour représentation paramétrique :
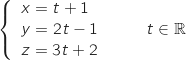
 la droite ayant pour représentation paramétrique :
la droite ayant pour représentation paramétrique :
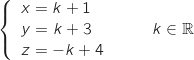
 le plan d'équation
le plan d'équation 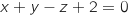 .
.
Question 1
Proposition a : Les droites et
et  sont parallèles.
Proposition b : Les droites
sont parallèles.
Proposition b : Les droites  et
et  sont coplanaires.
Proposition c : Le point C appartient à la droite
sont coplanaires.
Proposition c : Le point C appartient à la droite  .
Proposition d : Les droites
.
Proposition d : Les droites  et
et  sont orthogonales.
sont orthogonales.
Par lecture directe sur les représentations paramétriques :
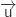 et
et 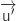 ne sont pas colinéaires ce qui élimine la réponse a.
Pendant qu'on travaille avec les vecteurs directeurs on peut "tenter" le produit scalaire pour savoir si les droites sont orthogonales :
ne sont pas colinéaires ce qui élimine la réponse a.
Pendant qu'on travaille avec les vecteurs directeurs on peut "tenter" le produit scalaire pour savoir si les droites sont orthogonales :
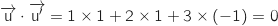 Donc les vecteurs directeurs des droites
Donc les vecteurs directeurs des droites  et
et  sont orthogonaux ce qui prouve que
sont orthogonaux ce qui prouve que  et
et  sont orthogonales.
La bonne réponse est la réponse d.
sont orthogonales.
La bonne réponse est la réponse d.
- un vecteur directeur de
 est
est 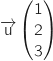
- un vecteur directeur de
 est
est 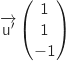
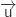 et
et 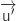 ne sont pas colinéaires ce qui élimine la réponse a.
Pendant qu'on travaille avec les vecteurs directeurs on peut "tenter" le produit scalaire pour savoir si les droites sont orthogonales :
ne sont pas colinéaires ce qui élimine la réponse a.
Pendant qu'on travaille avec les vecteurs directeurs on peut "tenter" le produit scalaire pour savoir si les droites sont orthogonales :
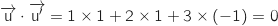 Donc les vecteurs directeurs des droites
Donc les vecteurs directeurs des droites  et
et  sont orthogonaux ce qui prouve que
sont orthogonaux ce qui prouve que  et
et  sont orthogonales.
La bonne réponse est la réponse d.
sont orthogonales.
La bonne réponse est la réponse d.
Question 2
Proposition a : Le plan contient la droite
contient la droite  et est parallèle à la droite
et est parallèle à la droite  .
Proposition b : Le plan
.
Proposition b : Le plan  contient la droite
contient la droite  et est parallèle à la droite
et est parallèle à la droite  .
Proposition c : Le plan
.
Proposition c : Le plan  contient la droite
contient la droite  et est orthogonal à la droite
et est orthogonal à la droite  .
Proposition d : Le plan
.
Proposition d : Le plan  contient les droites
contient les droites  et
et  .
.
Par lecture directe sur l'équation cartésienne un vecteur normal au plan  est
est 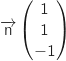 .
On remarque immédiatement que
.
On remarque immédiatement que 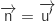 , c'est à dire que
, c'est à dire que  est aussi un vecteur directeur de
est aussi un vecteur directeur de  . Il
en résulte que la droite
. Il
en résulte que la droite  est orthogonale au plan
est orthogonale au plan  ce qui élimine toutes les réponses sauf la c. (on n'a même pas besoin de vérifier que
ce qui élimine toutes les réponses sauf la c. (on n'a même pas besoin de vérifier que  est incluse dans
est incluse dans  ).
La bonne réponse est la réponse c.
).
La bonne réponse est la réponse c.
 est
est 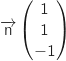 .
On remarque immédiatement que
.
On remarque immédiatement que 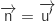 , c'est à dire que
, c'est à dire que  est aussi un vecteur directeur de
est aussi un vecteur directeur de  . Il
en résulte que la droite
. Il
en résulte que la droite  est orthogonale au plan
est orthogonale au plan  ce qui élimine toutes les réponses sauf la c. (on n'a même pas besoin de vérifier que
ce qui élimine toutes les réponses sauf la c. (on n'a même pas besoin de vérifier que  est incluse dans
est incluse dans  ).
La bonne réponse est la réponse c.
).
La bonne réponse est la réponse c.
Question 3
Proposition a : Les points A, D et C sont alignés. Proposition b : Le triangle ABC est rectangle en A. Proposition c : Le triangle ABC est équilatéral. Proposition d : Le point D est le milieu du segment [AB].
On peut commencer par calculer les coordonnées des vecteurs 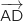 et
et 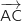 pour savoir si la réponse a. est bonne ou non :
pour savoir si la réponse a. est bonne ou non :
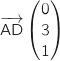
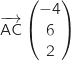 Ces vecteurs ne sont pas colinéaires donc on peut éliminer la réponse a.
Pour savoir si b. et c. sont vraies on calcule les longueurs des côtés du triangle ABC :
AB
Ces vecteurs ne sont pas colinéaires donc on peut éliminer la réponse a.
Pour savoir si b. et c. sont vraies on calcule les longueurs des côtés du triangle ABC :
AB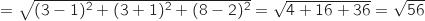 AC
AC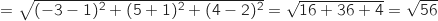 BC
BC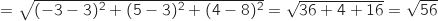 Donc AB
Donc AB AC
AC BC
BC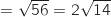 , ce qui montre que ABC est équilatéral.
La bonne réponse est la réponse c.
, ce qui montre que ABC est équilatéral.
La bonne réponse est la réponse c.
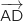 et
et 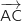 pour savoir si la réponse a. est bonne ou non :
pour savoir si la réponse a. est bonne ou non :
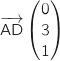
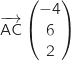 Ces vecteurs ne sont pas colinéaires donc on peut éliminer la réponse a.
Pour savoir si b. et c. sont vraies on calcule les longueurs des côtés du triangle ABC :
AB
Ces vecteurs ne sont pas colinéaires donc on peut éliminer la réponse a.
Pour savoir si b. et c. sont vraies on calcule les longueurs des côtés du triangle ABC :
AB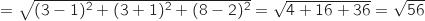 AC
AC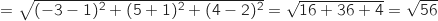 BC
BC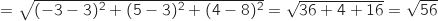 Donc AB
Donc AB AC
AC BC
BC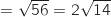 , ce qui montre que ABC est équilatéral.
La bonne réponse est la réponse c.
, ce qui montre que ABC est équilatéral.
La bonne réponse est la réponse c.
Question 4
On note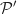 le plan contenant la droite
le plan contenant la droite  et le point A. Un vecteur normal à ce plan est :
Proposition a :
et le point A. Un vecteur normal à ce plan est :
Proposition a : 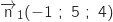 Proposition b :
Proposition b : 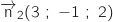 Proposition c :
Proposition c : 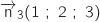 Proposition d :
Proposition d : 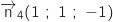
Un vecteur normal de 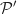 doit être orthogonal à deux vecteurs non colinéaires du plan. Comme
doit être orthogonal à deux vecteurs non colinéaires du plan. Comme  est dans le plan, un vecteur de
est dans le plan, un vecteur de 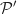 est
est
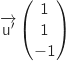 .
On peut déjà éliminer
.
On peut déjà éliminer 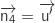 (
(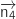 ne peut pas être orthogonal à lui-même).
On calcule maintenant les produits scalaires :
ne peut pas être orthogonal à lui-même).
On calcule maintenant les produits scalaires :
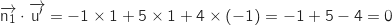 Donc
Donc 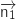 est un bon candidat.
est un bon candidat.
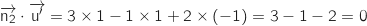 Donc
Donc 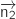 est aussi un bon candidat.
est aussi un bon candidat.
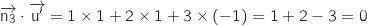 Donc
Donc 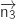 aussi !
On détermine les coordonnées d'un deuxième vecteur du plan. Pour cela on considère le point A'
aussi !
On détermine les coordonnées d'un deuxième vecteur du plan. Pour cela on considère le point A'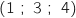 de la droite
de la droite  (obtenu en remplaçant
(obtenu en remplaçant
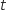 par 0 dans la représentation paramétrique) et on calcule les coordonnées de
par 0 dans la représentation paramétrique) et on calcule les coordonnées de 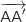 .
.
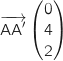 On remarque au passage que ce vecteur n'est pas colinéaire à
On remarque au passage que ce vecteur n'est pas colinéaire à 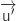 , on calcule de nouveau les produits scalaires :
, on calcule de nouveau les produits scalaires :
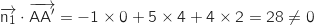
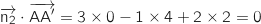
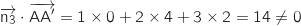 Donc le seul vecteur orthogonal à deux vecteurs non colinéaires du plan
Donc le seul vecteur orthogonal à deux vecteurs non colinéaires du plan 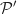 est le vecteur
est le vecteur 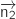 .
La bonne réponse est la réponse b.
.
La bonne réponse est la réponse b.
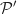 doit être orthogonal à deux vecteurs non colinéaires du plan. Comme
doit être orthogonal à deux vecteurs non colinéaires du plan. Comme  est dans le plan, un vecteur de
est dans le plan, un vecteur de 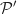 est
est
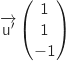 .
On peut déjà éliminer
.
On peut déjà éliminer 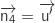 (
(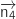 ne peut pas être orthogonal à lui-même).
On calcule maintenant les produits scalaires :
ne peut pas être orthogonal à lui-même).
On calcule maintenant les produits scalaires :
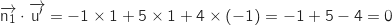 Donc
Donc 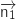 est un bon candidat.
est un bon candidat.
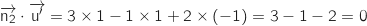 Donc
Donc 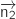 est aussi un bon candidat.
est aussi un bon candidat.
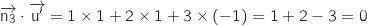 Donc
Donc 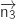 aussi !
On détermine les coordonnées d'un deuxième vecteur du plan. Pour cela on considère le point A'
aussi !
On détermine les coordonnées d'un deuxième vecteur du plan. Pour cela on considère le point A'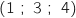 de la droite
de la droite  (obtenu en remplaçant
(obtenu en remplaçant
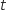 par 0 dans la représentation paramétrique) et on calcule les coordonnées de
par 0 dans la représentation paramétrique) et on calcule les coordonnées de 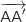 .
.
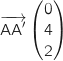 On remarque au passage que ce vecteur n'est pas colinéaire à
On remarque au passage que ce vecteur n'est pas colinéaire à 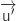 , on calcule de nouveau les produits scalaires :
, on calcule de nouveau les produits scalaires :
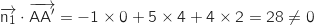
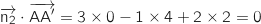
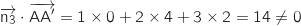 Donc le seul vecteur orthogonal à deux vecteurs non colinéaires du plan
Donc le seul vecteur orthogonal à deux vecteurs non colinéaires du plan 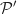 est le vecteur
est le vecteur 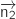 .
La bonne réponse est la réponse b.
.
La bonne réponse est la réponse b.
