Sujet et corrigé de l'exercice 3 du bac S de maths de mai 2013 au Liban
Cacher les corrigés
Etant donné un nombre réel , on considère la fonction
, on considère la fonction 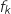 définie sur
définie sur  par
par
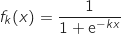
 .
.
Partie A
Dans cette partie on choisit . On a donc, pour tout réel
. On a donc, pour tout réel 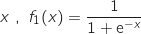 .
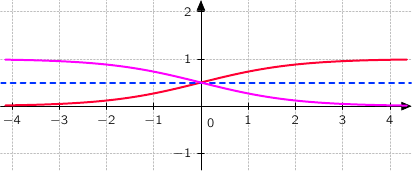
La représentation graphique
.
La représentation graphique 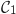 de la fonction
de la fonction 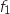 dans le repère
dans le repère 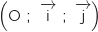 est donnée ci-dessous :
est donnée ci-dessous :
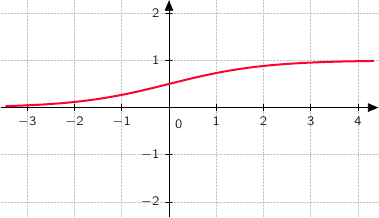
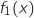 en
en 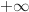 et en
et en 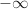 et interpréter graphiquement les résultats obtenus.
et interpréter graphiquement les résultats obtenus.
Limite en 
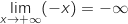 et par composition
et par composition 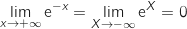 par valeurs positives.
En rajoutant 1 puis en inversant on obtient
par valeurs positives.
En rajoutant 1 puis en inversant on obtient 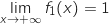 .
On en déduit que la courbe de
.
On en déduit que la courbe de  admet en
admet en  une asymptote horizontale d'équation
une asymptote horizontale d'équation 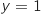 .
Limite en
.
Limite en 
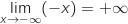 et par composition
et par composition 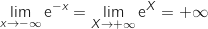 .
Du coup,
.
Du coup, 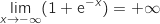 et par inversion
et par inversion 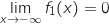 par valeurs positives.
La courbe représentative de
par valeurs positives.
La courbe représentative de 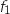 admet en
admet en  une asymptote horizontale d'équation
une asymptote horizontale d'équation 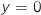 (axe des abscisses).
(axe des abscisses).

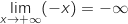 et par composition
et par composition 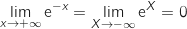 par valeurs positives.
En rajoutant 1 puis en inversant on obtient
par valeurs positives.
En rajoutant 1 puis en inversant on obtient 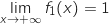 .
On en déduit que la courbe de
.
On en déduit que la courbe de 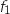 admet en
admet en  une asymptote horizontale d'équation
une asymptote horizontale d'équation 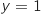 .
Limite en
.
Limite en 
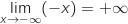 et par composition
et par composition 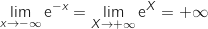 .
Du coup,
.
Du coup, 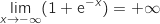 et par inversion
et par inversion 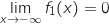 par valeurs positives.
La courbe représentative de
par valeurs positives.
La courbe représentative de 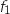 admet en
admet en  une asymptote horizontale d'équation
une asymptote horizontale d'équation 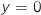 (axe des abscisses).
(axe des abscisses).
2. Démontrer que, pour tout réel
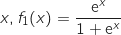 .
.
Pour tout réel  :
: 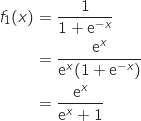
3. On appelle  :
: 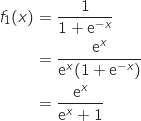
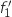 la fonction dérivée de
la fonction dérivée de 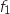 sur
sur  . Calculer, pour tout réel
. Calculer, pour tout réel 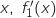 .
En déduire les variations de la fonction
.
En déduire les variations de la fonction 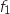 sur
sur  .
.
La fonction 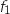 est dérivable sur
est dérivable sur  et on peut écrire :
et on peut écrire : 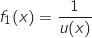 avec :
avec :
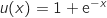 et
et 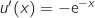 Donc on a :
Donc on a : 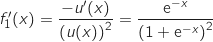 Pour tout
Pour tout  ;
; 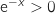 , de même
, de même 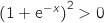 , donc
, donc 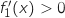 et la fonction
et la fonction 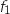 est strictement croissante sur
est strictement croissante sur  .
.
4. On définit le nombre 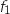 est dérivable sur
est dérivable sur  et on peut écrire :
et on peut écrire : 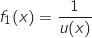 avec :
avec :
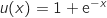 et
et 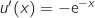 Donc on a :
Donc on a : 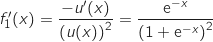 Pour tout
Pour tout  ;
; 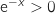 , de même
, de même 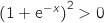 , donc
, donc 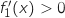 et la fonction
et la fonction 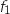 est strictement croissante sur
est strictement croissante sur  .
.
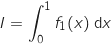 .
Montrer que
.
Montrer que 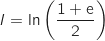 . Donner une interprétation graphique de
. Donner une interprétation graphique de 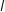 .
.
Pour calculer cette intégrale on commence par déterminer une primitive de 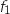 . Il est plus facile de travailler avec l'expression
. Il est plus facile de travailler avec l'expression 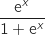 où
l'on peut "voir"
où
l'on peut "voir" 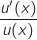 avec
avec 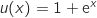 et
et 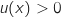 pour tout
pour tout  .
Du coup une primitive sur
.
Du coup une primitive sur  de
de  est définie par
est définie par 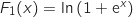 .
Maintenant on peut calculer
.
Maintenant on peut calculer  :
:
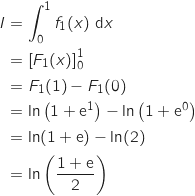 La fonction
La fonction 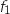 étant positive sur
étant positive sur  ,
,  représente, en unités d'aire, l'aire du domaine délimité par l'axe des ordonnées
, la droite d'équation
représente, en unités d'aire, l'aire du domaine délimité par l'axe des ordonnées
, la droite d'équation  , l'axe des abscisses et la courbe représentative de
, l'axe des abscisses et la courbe représentative de 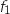 .
.
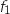 . Il est plus facile de travailler avec l'expression
. Il est plus facile de travailler avec l'expression 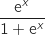 où
l'on peut "voir"
où
l'on peut "voir" 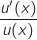 avec
avec 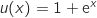 et
et 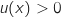 pour tout
pour tout  .
Du coup une primitive sur
.
Du coup une primitive sur  de
de 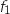 est définie par
est définie par 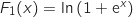 .
Maintenant on peut calculer
.
Maintenant on peut calculer 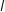 :
:
 La fonction
La fonction 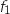 étant positive sur
étant positive sur  ,
, 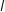 représente, en unités d'aire, l'aire du domaine délimité par l'axe des ordonnées
, la droite d'équation
représente, en unités d'aire, l'aire du domaine délimité par l'axe des ordonnées
, la droite d'équation  , l'axe des abscisses et la courbe représentative de
, l'axe des abscisses et la courbe représentative de 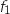 .
.
Partie B
Dans cette partie, on choisit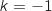 et on souhaite tracer la courbe
et on souhaite tracer la courbe 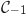 représentant la fonction
représentant la fonction 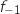 .
Pour tout réel
.
Pour tout réel  , on appelle P le point de
, on appelle P le point de 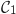 d'abscisse
d'abscisse  et M le point de
et M le point de  d'abscisse
d'abscisse  .
On note K le milieu du segment [MP].
1. Montrer que, pour tout réel
.
On note K le milieu du segment [MP].
1. Montrer que, pour tout réel 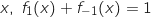 .
.
Pour tout réel  :
:
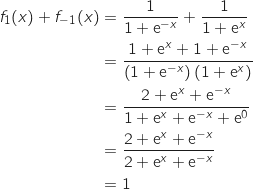
2. En déduire que le point K appartient à la droite d'équation  :
:
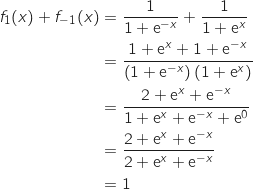
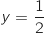 .
.
On a les coordonnées suivantes : P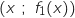 et M
et M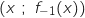 .
Du coup les coordonnées du milieu K de [MP] sont :
K
.
Du coup les coordonnées du milieu K de [MP] sont :
K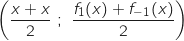 soit K
soit K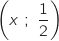 .
Donc le point K appartient à la droite d'équation
.
Donc le point K appartient à la droite d'équation 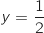 .
.
3. Tracer la courbe 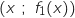 et M
et M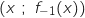 .
Du coup les coordonnées du milieu K de [MP] sont :
K
.
Du coup les coordonnées du milieu K de [MP] sont :
K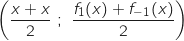 soit K
soit K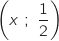 .
Donc le point K appartient à la droite d'équation
.
Donc le point K appartient à la droite d'équation 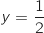 .
.
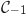 sur le graphique.
sur le graphique.
On trace la droite d'équation 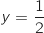 . D'après ce qui précède les courbes
. D'après ce qui précède les courbes 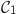 et
et 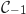 sont symétriques
par rapport à cette droite ce qui permet de construire
sont symétriques
par rapport à cette droite ce qui permet de construire 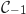 .
.
4. En déduire l'aire, en unités d'aire, du domaine délimité par les courbes 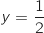 . D'après ce qui précède les courbes
. D'après ce qui précède les courbes 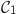 et
et 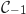 sont symétriques
par rapport à cette droite ce qui permet de construire
sont symétriques
par rapport à cette droite ce qui permet de construire 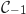 .
.

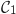 ,
, 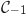 l'axe des ordonnées et la droite d'équation
l'axe des ordonnées et la droite d'équation 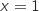 .
.
On remarque déjà que : 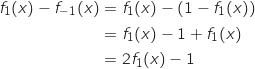 Comme
Comme 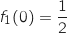 et comme
et comme 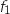 est strictement croissante, pour tout
est strictement croissante, pour tout 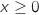 ,
, 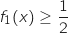 et donc
et donc 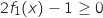 . Il en résulte que
sur
. Il en résulte que
sur  ,
, 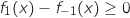 ce qui entraîne que
ce qui entraîne que 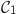 est située au dessus de
est située au dessus de 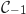 .
Ainsi l'aire considérée se calcule en effectuant :
.
Ainsi l'aire considérée se calcule en effectuant :
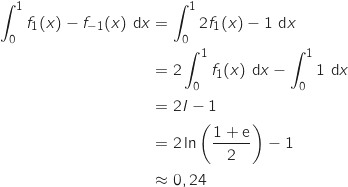
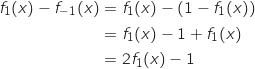 Comme
Comme 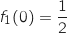 et comme
et comme 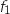 est strictement croissante, pour tout
est strictement croissante, pour tout 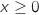 ,
, 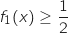 et donc
et donc 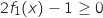 . Il en résulte que
sur
. Il en résulte que
sur  ,
, 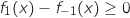 ce qui entraîne que
ce qui entraîne que 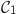 est située au dessus de
est située au dessus de 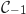 .
Ainsi l'aire considérée se calcule en effectuant :
.
Ainsi l'aire considérée se calcule en effectuant :
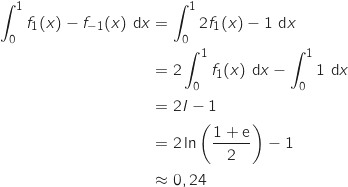
Partie C
Dans cette partie, on ne privilégie pas de valeur particulière du paramètre .
Pour chacune des affirmations suivantes, dire si elle est vraie ou fausse et justifier la réponse.
1. Quelle que soit la valeur du nombre réel
.
Pour chacune des affirmations suivantes, dire si elle est vraie ou fausse et justifier la réponse.
1. Quelle que soit la valeur du nombre réel  , la représentation graphique de la fonction
, la représentation graphique de la fonction 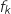 est strictement comprise entre les droites d'équations
est strictement comprise entre les droites d'équations 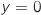 et
et 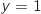 .
.
Pour tout  et tout
et tout 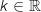 ;
; 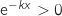 et du coup
et du coup 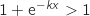 , donc on a :
, donc on a :
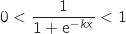 soit
soit 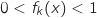 , ce qui prouve que la courbe de
, ce qui prouve que la courbe de 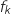 est strictement comprise entre les droites d'équations
est strictement comprise entre les droites d'équations
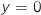 et
et 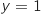 .
L'affirmation est VRAIE.
.
L'affirmation est VRAIE.
2. Quelle que soit la valeur du réel  et tout
et tout 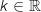 ;
; 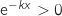 et du coup
et du coup 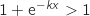 , donc on a :
, donc on a :
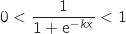 soit
soit 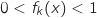 , ce qui prouve que la courbe de
, ce qui prouve que la courbe de 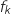 est strictement comprise entre les droites d'équations
est strictement comprise entre les droites d'équations
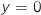 et
et 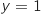 .
L'affirmation est VRAIE.
.
L'affirmation est VRAIE.
 , la fonction
, la fonction 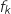 est strictement croissante.
est strictement croissante.
Pour tout  et tout
et tout 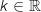 la fonction
la fonction 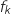 est dérivable et on a :
est dérivable et on a :
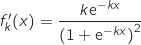 Ainsi la dérivée à le même signe que
Ainsi la dérivée à le même signe que  , donc la fonction
, donc la fonction 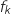 est strictement décroissante pour
est strictement décroissante pour 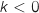 ; constante pour
; constante pour 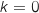 et strictement croissante pour
et strictement croissante pour 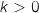 .
L'affirmation est FAUSSE.
.
L'affirmation est FAUSSE.
3. Pour tout réel  et tout
et tout 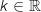 la fonction
la fonction 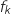 est dérivable et on a :
est dérivable et on a :
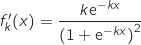 Ainsi la dérivée à le même signe que
Ainsi la dérivée à le même signe que  , donc la fonction
, donc la fonction 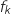 est strictement décroissante pour
est strictement décroissante pour 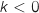 ; constante pour
; constante pour 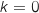 et strictement croissante pour
et strictement croissante pour 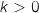 .
L'affirmation est FAUSSE.
.
L'affirmation est FAUSSE.
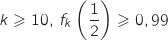 .
.
Pour tout réel  on a
on a 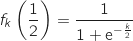 Considérons la fonction
Considérons la fonction  définie sur
définie sur  par
par 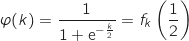 .
On peut remarquer que
.
On peut remarquer que 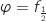 , donc
, donc  est croissante d'après la question précédente.
On calcule
est croissante d'après la question précédente.
On calcule 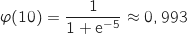 .
Comme
.
Comme  est croissante, pour tout
est croissante, pour tout 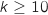 ;
; 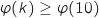 , soit
, soit 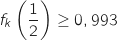 .
L'affirmation est VRAIE.
.
L'affirmation est VRAIE.
 on a
on a 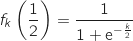 Considérons la fonction
Considérons la fonction  définie sur
définie sur  par
par 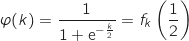 .
On peut remarquer que
.
On peut remarquer que 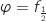 , donc
, donc  est croissante d'après la question précédente.
On calcule
est croissante d'après la question précédente.
On calcule 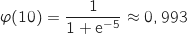 .
Comme
.
Comme  est croissante, pour tout
est croissante, pour tout 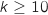 ;
; 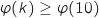 , soit
, soit 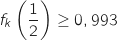 .
L'affirmation est VRAIE.
.
L'affirmation est VRAIE.
