Sujet et corrigé de l'exercice 4 du bac S de maths de mai 2013 au Liban
Cacher les corrigés
On considère la suite numérique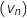 définie pour tout entier naturel
définie pour tout entier naturel  par
par
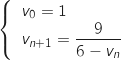
Partie A
1. On souhaite écrire un algorithme affichant, pour un entier naturel donné, tous les termes de la suite, du rang
donné, tous les termes de la suite, du rang 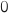 au rang
au rang  .
Parmi les trois algorithmes suivants, un seul convient. Préciser lequel en justifiant la réponse.
.
Parmi les trois algorithmes suivants, un seul convient. Préciser lequel en justifiant la réponse.
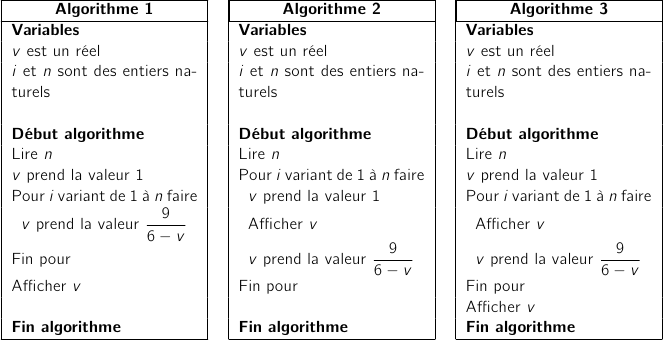
L'algorithme numéro 1 ne convient pas car l'affichage ne figure pas dans la boucle et donc cet algorithme ne va afficher que le terme de rang  saisi par l'utilisateur.
L'algorithme 2 ne convient pas non plus. En effet
saisi par l'utilisateur.
L'algorithme 2 ne convient pas non plus. En effet  est réinitialisé à 1 à chaque tour de boucle, donc cet algorithme va provoquer l'affichage d'une simple série de 1.
Par élimination le bon algorithme est le numéro 3. On pourra noter que l'instruction d'affichage incluse dans la boucle affiche les termes du rang 0 au rang
est réinitialisé à 1 à chaque tour de boucle, donc cet algorithme va provoquer l'affichage d'une simple série de 1.
Par élimination le bon algorithme est le numéro 3. On pourra noter que l'instruction d'affichage incluse dans la boucle affiche les termes du rang 0 au rang 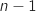 . L'instruction
d'affichage tout en fin d'algorithme est indispensable pour afficher le terme de rang
. L'instruction
d'affichage tout en fin d'algorithme est indispensable pour afficher le terme de rang  .
.
2. Pour  saisi par l'utilisateur.
L'algorithme 2 ne convient pas non plus. En effet
saisi par l'utilisateur.
L'algorithme 2 ne convient pas non plus. En effet  est réinitialisé à 1 à chaque tour de boucle, donc cet algorithme va provoquer l'affichage d'une simple série de 1.
Par élimination le bon algorithme est le numéro 3. On pourra noter que l'instruction d'affichage incluse dans la boucle affiche les termes du rang 0 au rang
est réinitialisé à 1 à chaque tour de boucle, donc cet algorithme va provoquer l'affichage d'une simple série de 1.
Par élimination le bon algorithme est le numéro 3. On pourra noter que l'instruction d'affichage incluse dans la boucle affiche les termes du rang 0 au rang 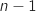 . L'instruction
d'affichage tout en fin d'algorithme est indispensable pour afficher le terme de rang
. L'instruction
d'affichage tout en fin d'algorithme est indispensable pour afficher le terme de rang  .
.
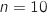 on obtient l'affichage suivant :
on obtient l'affichage suivant :

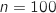 , les derniers termes affichés sont :
, les derniers termes affichés sont :

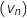 ?
?
On peut conjecturer que la suite  est croissante et converge vers une limite proche de 2,97.
est croissante et converge vers une limite proche de 2,97.
 est croissante et converge vers une limite proche de 2,97.
est croissante et converge vers une limite proche de 2,97.
3.a. Démontrer par récurrence que, pour tout entier naturel
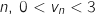 .
.
La propriété à montrer pour tout entier 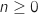 est :
est :  : «
: « 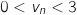 ».
Initialisation au rang 0
».
Initialisation au rang 0
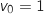 et on a bien
et on a bien 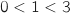 , donc
, donc 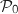 est vraie.
Hérédité
On suppose que
est vraie.
Hérédité
On suppose que 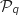 est vraie à un rang
est vraie à un rang  ce qui donne l'hypothèse de récurrence :
ce qui donne l'hypothèse de récurrence : 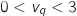 .
On veut montrer qu'alors
.
On veut montrer qu'alors  est vraie.
On sait par définition de la suite que
est vraie.
On sait par définition de la suite que 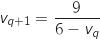 , en partant de l'hypothèse de récurrence on « construit » ce
, en partant de l'hypothèse de récurrence on « construit » ce 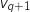 :
:
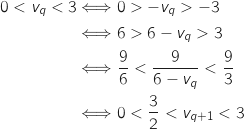 Donc
Donc  est vraie et la propriété est héréditaire, comme elle est initialisée au rang 0, on en déduit qu'elle est vraie pour tout entier naturel
est vraie et la propriété est héréditaire, comme elle est initialisée au rang 0, on en déduit qu'elle est vraie pour tout entier naturel  .
.
Démontrer que, pour tout entier naturel 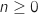 est :
est :  : «
: « 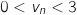 ».
Initialisation au rang 0
».
Initialisation au rang 0
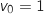 et on a bien
et on a bien 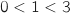 , donc
, donc 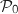 est vraie.
Hérédité
On suppose que
est vraie.
Hérédité
On suppose que 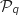 est vraie à un rang
est vraie à un rang  ce qui donne l'hypothèse de récurrence :
ce qui donne l'hypothèse de récurrence : 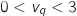 .
On veut montrer qu'alors
.
On veut montrer qu'alors  est vraie.
On sait par définition de la suite que
est vraie.
On sait par définition de la suite que 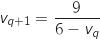 , en partant de l'hypothèse de récurrence on « construit » ce
, en partant de l'hypothèse de récurrence on « construit » ce 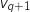 :
:
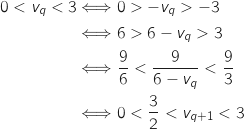 Donc
Donc  est vraie et la propriété est héréditaire, comme elle est initialisée au rang 0, on en déduit qu'elle est vraie pour tout entier naturel
est vraie et la propriété est héréditaire, comme elle est initialisée au rang 0, on en déduit qu'elle est vraie pour tout entier naturel  .
.
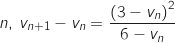 .
La suite
.
La suite 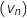 est-elle monotone ?
est-elle monotone ?
Pour tout entier naturel  :
:

c. Démontrer que la suite  :
:

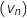 est convergente.
est convergente.
Dans a. on a vu que pour tout entier naturel  ;
; 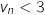 du coup
du coup 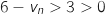 et comme
et comme 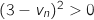 on en déduit grâce
à l'expression de la question b. que
on en déduit grâce
à l'expression de la question b. que 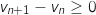 et donc que
et donc que  est croissante.
Ainsi la suite est croissante et majorée par 3, il en résulte d'après le théorème de convergence monotone que
est croissante.
Ainsi la suite est croissante et majorée par 3, il en résulte d'après le théorème de convergence monotone que  est convergente.
est convergente.
 ;
; 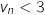 du coup
du coup 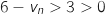 et comme
et comme 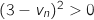 on en déduit grâce
à l'expression de la question b. que
on en déduit grâce
à l'expression de la question b. que 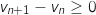 et donc que
et donc que  est croissante.
Ainsi la suite est croissante et majorée par 3, il en résulte d'après le théorème de convergence monotone que
est croissante.
Ainsi la suite est croissante et majorée par 3, il en résulte d'après le théorème de convergence monotone que  est convergente.
est convergente.
Partie B
On considère la suite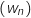 définie pour tout
définie pour tout  entier naturel par
entier naturel par
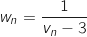
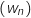 est une suite arithmétique de raison
est une suite arithmétique de raison 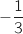 .
.
Pour tout entier naturel  on a :
on a :
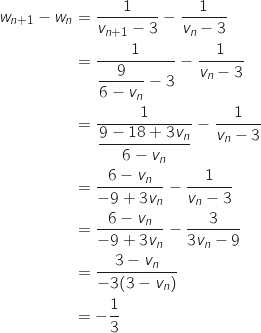 Donc
Donc 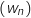 est bien une suite arihtmétique de raison
est bien une suite arihtmétique de raison 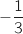 .
.
2. En déduire l'expression de  on a :
on a :
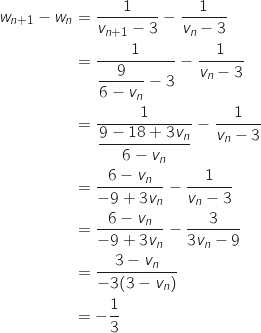 Donc
Donc 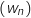 est bien une suite arihtmétique de raison
est bien une suite arihtmétique de raison 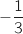 .
.
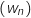 , puis celle de
, puis celle de 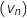 en fonction de
en fonction de  .
.
Pour tout entier naturel  on a :
on a :
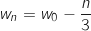 avec
avec 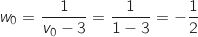 .
Donc finalement,
.
Donc finalement, 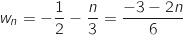 .
.
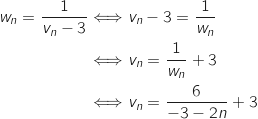
3. Déterminer la limite de la suite  on a :
on a :
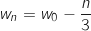 avec
avec 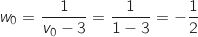 .
Donc finalement,
.
Donc finalement, 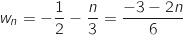 .
.
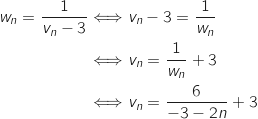
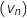 .
.
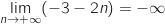 ; par quotient
; par quotient 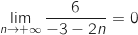 et finalement en
ajoutant 3 on obtient
et finalement en
ajoutant 3 on obtient 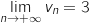 .
.
