Sujet et corrigé de l'exercice 3 du bac S de maths de mai 2014 au Liban
Cacher les corrigés
Soit la fonction définie sur l'intervalle par
On note la courbe représentative de dans un repère orthogonal.
Partie A
1. On note la fonction dérivée de la fonction sur l'intervalle .
Pour tout réel de l'intervalle , calculer .
En déduire les variations de la fonction sur l'intervalle .
est dérivable sur et on a :
avec :
;
;
Donc
Pour tout , , donc a le même signe que ce qui donne le tableau de variations :
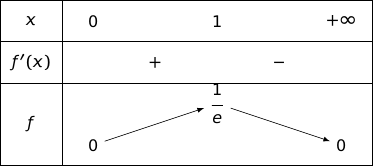
;
Pour voir question suivante.
2. Déterminer la limite de la fonction en .
Quelle interprétation graphique peut-on faire de ce résultat ?
On écrit
(limite connue),
donc par inverse :
Du coup la courbe représentative de admet l'axe des abscisses comme asymptote en .
Partie B
Soit la fonction définie sur l'intervalle de la façon suivante :
Pour tout réel de l'intervalle , est l'aire, en unités d'aire, du domaine délimité par l'axe des abscisses, la courbe et les droites d'équations et .
1. Déterminer le sens de variation de la fonction .
La fonction est continue sur et d'après l'étude précédente elle est également positive sur cet intervalle donc on peut écrire pour tout :
Du coup et comme pour tout , , la fonction est croissante sur .
2. On admet que l'aire du domaine délimité par la courbe et l'axe des abscisses est égale à 1 unité d'aire.
Que peut-on en déduire pour la fonction ?
On en déduit que .
3. On cherche à prouver l'existence d'un nombre réel tel que la droite d'équation partage le domaine compris entre l'axe des abscisses et la courbe , en deux parties de même aire, et à trouver une valeur approchée de ce réel.
a. Démontrer que l'équation admet une unique solution sur l'intervalle .
On a le tableau de variations :
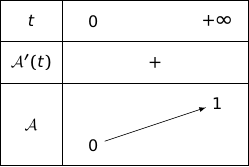
La fonction est définie, continue et strictement croissante sur avec :
et
or , donc d'après le théorème de la valeur intermédiaire il existe un unique tel que .
b. Sur le graphique ci-dessous sont tracées la courbe , ainsi que la courbe représentant la fonction .
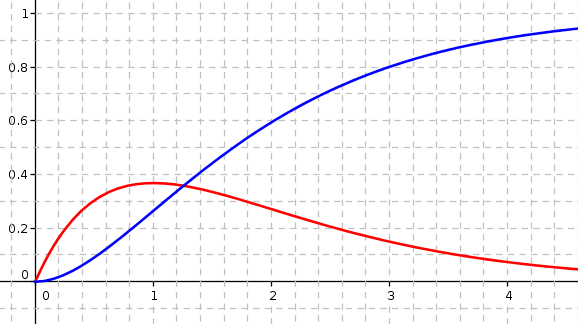
Identifier les courbes et , puis tracer la droite d'équation .
En déduire une valeur approchée du réel .
Hachurer le domaine correspondant à .
On identifie facilement et grâce aux variations.
Par lecture graphique l'antécédent par de est
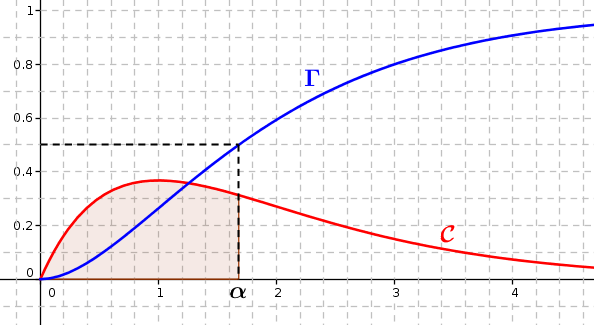
4. On définit la fonction sur l'intervalle par :
a. On note la fonction dérivée de la fonction sur l'intervalle .
Pour tout réel de l'intervalle , calculer .
La fonction est dérivable sur et on a :
avec :
;
;
D'où
Donc est une primitive de .
b. En déduire, pour tout réel de l'intervalle , une expression de .
c. Calculer une valeur approchée à près de .
.
