Corrigé de l'exercice 2 de maths du bac S de juin 2011 en métropole
Cacher les corrigés
Pour chaque question, une seule des quatre réponses proposées est exacte. Le candidat indiquera sur la copie le numéro de la question et la réponse choisie. Chaque réponse exacte rapporte un point. Aucune justification n'est demandée. Aucun point n'est enlevé en l'absence de réponse ou en cas de réponse fausse. Le plan complexe est rapporté au repère orthonormal direct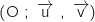
.
On désigne par A, B, C, D les points d'affixes respectives 
.
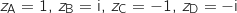Dans le sujet original, la première question portait sur les rotations qui ne sont plus au programme à partir de la session
2013 du baccalauréat.
2. L'ensemble des points d'affixe 
telle que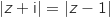 
est :
- la médiatrice du segment [BC],
- le milieu du segment [BC],
- le cercle de centre O et de rayon 1,
- la médiatrice du segment [AD].
La bonne réponse est la médiatrice du segment [AD].
En effet on interprètant la relation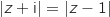 
en terme de distance, on obtient l'ensemble des points M d'affixe tels que MD
MA, c'est à dire la médiatrice de [AD].
A remarquer que la droite en question est également la médiatrice de [BC], donc la première réponse est également valide.
3. L'ensemble des points d'affixe 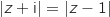en terme de distance, on obtient l'ensemble des points M d'affixe tels que MDMA, c'est à dire la médiatrice de [AD].
A remarquer que la droite en question est également la médiatrice de [BC], donc la première réponse est également valide.
telle que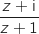 
soit un imaginaire pur est :
- la droite (CD) privée du point C,
- le cercle de diamètre [CD] privé du point C,
- le cercle de diamètre [BD] privé du point C,
- la médiatrice du segment [AB].
La bonne réponse est le cercle de diamètre [CD] privé du point C.
En effet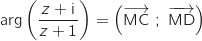 
, donc 
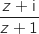imaginaire pur entraîne que
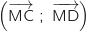est un angle droit (avec M
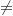C et M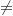D), cela caractérise les points du cercle de diamètre [CD] privé des points
C et D.
On remarque, de plus, que le point D d'affixe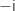 
appartient à l'ensemble cherché car 
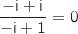est un imaginaire pur, (en revanche le point C d'affixe 
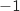ne peut pas appartenir à l'ensemble de points cherché car le rapport 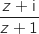n'est pas défini pour 
).
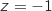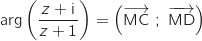, donc 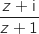imaginaire pur entraîne que
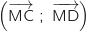est un angle droit (avec M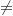C et M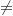D), cela caractérise les points du cercle de diamètre [CD] privé des points
C et D.
On remarque, de plus, que le point D d'affixe 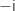appartient à l'ensemble cherché car 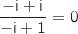est un imaginaire pur, (en revanche le point C d'affixe 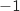ne peut pas appartenir à l'ensemble de points cherché car le rapport 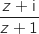n'est pas défini pour ).
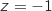4. L'ensemble des points d'affixe
telle que arg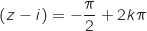
où 
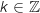est :
- le demi-cercle de diamètre [BD] passant par A,
- la droite (BD),
- la demi-droite ]BD) d'origine B passant par D privée de B,
- le cercle de diamètre [BD] privé de B et D.
La bonne réponse est la demi-droite ]BD) d'origine B passant par D privée de B.
En effet,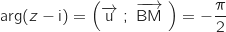 
, donc l'ensemble des points cherché se situe sur une demi-droite d'origine B (avec B exclu), perpendiculaire à l'axe 
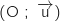, on remarque en outre que le point D d'affixe 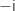appartient à l'ensemble cherché car 
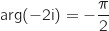, donc l'ensemble en question est la demi-droite ]BD).
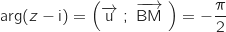, donc l'ensemble des points cherché se situe sur une demi-droite d'origine B (avec B exclu), perpendiculaire à l'axe 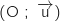, on remarque en outre que le point D d'affixe 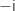appartient à l'ensemble cherché car 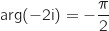, donc l'ensemble en question est la demi-droite ]BD).
