Corrigé de l'exercice 1 du bac S de maths de juin 2012 en métropole
Cacher les corrigés
Le plan est muni d'un repère orthonormé .
On considère une fonction
.
On considère une fonction  dérivable sur l'intervalle
dérivable sur l'intervalle 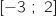 .
On dispose des informations suivantes:
.
On dispose des informations suivantes:
-
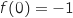 .
.
- la dérivée
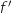 de la fonction
de la fonction  admet la courbe représentative
admet la courbe représentative 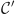 ci-dessous.
ci-dessous.
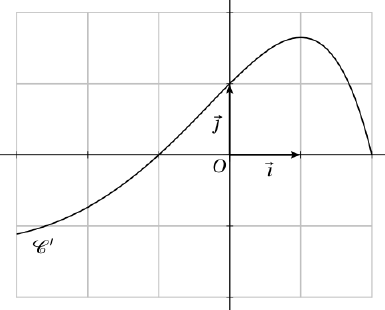
Pour chacune des affirmations suivantes, dire si elle est vraie ou fausse et justifier la réponse. 1. Pour tout réel
 de l'intervalle
de l'intervalle 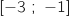 ,
, 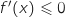 .
.
On remarque que sur 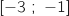 la courbe
la courbe 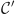 est située en dessous de l'axe des abscisses donc
est située en dessous de l'axe des abscisses donc 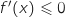 pour tout
pour tout 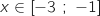 .
L'affirmation est VRAIE.
.
L'affirmation est VRAIE.
2. La fonction 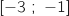 la courbe
la courbe 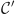 est située en dessous de l'axe des abscisses donc
est située en dessous de l'axe des abscisses donc 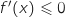 pour tout
pour tout 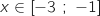 .
L'affirmation est VRAIE.
.
L'affirmation est VRAIE.
 est croissante sur l'intervalle
est croissante sur l'intervalle 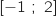 .
.
Sur l'intervalle 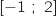 , par observation graphique on a :
, par observation graphique on a :
 est strictement croissante sur l'intervalle
est strictement croissante sur l'intervalle 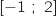 .
L'affirmation est VRAIE.
.
L'affirmation est VRAIE.
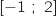 , par observation graphique on a :
, par observation graphique on a :
-
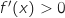 pour
pour 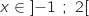
-
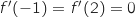
 est strictement croissante sur l'intervalle
est strictement croissante sur l'intervalle 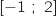 .
L'affirmation est VRAIE.
.
L'affirmation est VRAIE.
3. Pour tout réel
 de l'intervalle
de l'intervalle 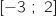 ,
, 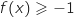 .
.
La fonction  est strictement croissante sur
est strictement croissante sur 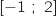 avec
avec 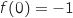 .
Donc pour tout
.
Donc pour tout 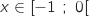 ,
, 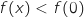 , soit
, soit 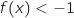 .
Donc l'affirmation est FAUSSE.
.
Donc l'affirmation est FAUSSE.
4. Soit  est strictement croissante sur
est strictement croissante sur 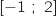 avec
avec 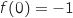 .
Donc pour tout
.
Donc pour tout 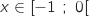 ,
, 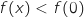 , soit
, soit 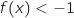 .
Donc l'affirmation est FAUSSE.
.
Donc l'affirmation est FAUSSE.
 la courbe représentative de la fonction
la courbe représentative de la fonction  .
La tangente à la courbe
.
La tangente à la courbe  au point d'abscisse 0 passe par le point de coordonnées
au point d'abscisse 0 passe par le point de coordonnées 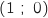 .
.
Le coefficient directeur de la tangente considérée est donné par 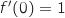 (obtenu par lecture graphique) et l'équation réduite de cette tangente est donc
(obtenu par lecture graphique) et l'équation réduite de cette tangente est donc
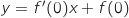 soit
soit 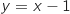 .
Les coordonnées du point
.
Les coordonnées du point 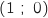 vérifient cette équation, donc la tangente passe bien par ce point.
L'affirmation est VRAIE.
vérifient cette équation, donc la tangente passe bien par ce point.
L'affirmation est VRAIE.
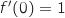 (obtenu par lecture graphique) et l'équation réduite de cette tangente est donc
(obtenu par lecture graphique) et l'équation réduite de cette tangente est donc
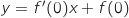 soit
soit 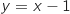 .
Les coordonnées du point
.
Les coordonnées du point 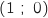 vérifient cette équation, donc la tangente passe bien par ce point.
L'affirmation est VRAIE.
vérifient cette équation, donc la tangente passe bien par ce point.
L'affirmation est VRAIE.
