Corrigé de l'exercice 2 du bac S de maths de juin 2012 en métropole
Cacher les corrigés
Pour embaucher ses cadres une entreprise fait appel à un cabinet de recrutement. La procédure retenue est la suivante. Le cabinet effectue une première sélection de candidats sur dossier. 40 % des dossiers reçus sont validés et transmis à l'entreprise. Les candidats ainsi sélectionnés passent un premier entretien à l'issue duquel 70 % d'entre eux sont retenus. Ces derniers sont convoqués à un ultime entretien avec le directeur des ressources humaines qui recrutera 25 % des candidats rencontrés.
1. On choisit au hasard le dossier d'un candidat. On considère les événements suivants :
- D : « Le candidat est retenu sur dossier »,
- E
 : « Le candidat est retenu à l'issue du premier entretien »,
: « Le candidat est retenu à l'issue du premier entretien »,
- E
 : « Le candidat est recruté ».
: « Le candidat est recruté ».
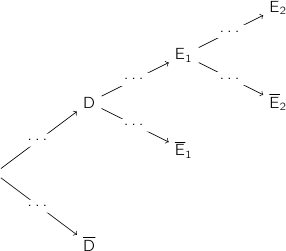
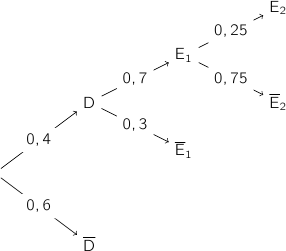
b. Calculer la probabilité de l'événement E
 .
.
On remarque que 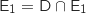 et d'après la formule des probabilités composées (principe multiplicatif sur l'arbre) on a :
et d'après la formule des probabilités composées (principe multiplicatif sur l'arbre) on a :
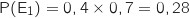
c. On note F l'événement « Le candidat n'est pas recruté ».
Démontrer que la probabilité de l'événement F est égale à 0,93.
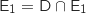 et d'après la formule des probabilités composées (principe multiplicatif sur l'arbre) on a :
et d'après la formule des probabilités composées (principe multiplicatif sur l'arbre) on a :
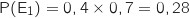
L'événement contraire de F est 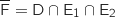 .
En utilisant le principe multiplicatif sur l'arbre on a :
.
En utilisant le principe multiplicatif sur l'arbre on a :
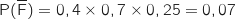 Donc
Donc 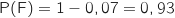 .
.
2. Cinq amis postulent à un emploi de cadre dans cette entreprise. Les études de leur dossier sont faites indépendamment les unes des autres.
On admet que la probabilité que chacun d'eux soit recruté est égale à 0,07.
On désigne par 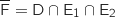 .
En utilisant le principe multiplicatif sur l'arbre on a :
.
En utilisant le principe multiplicatif sur l'arbre on a :
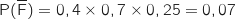 Donc
Donc 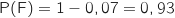 .
.
 la variable aléatoire donnant le nombre de personnes recrutées parmi ces cinq candidats.
a. Justifier que
la variable aléatoire donnant le nombre de personnes recrutées parmi ces cinq candidats.
a. Justifier que  suit une loi binomiale et préciser les paramètres de cette loi.
suit une loi binomiale et préciser les paramètres de cette loi.
On répète de façon indépendante 5 fois une expérience de Bernoulli dont la probabilité du succès est 0,07. Donc la variable aléatoire  qui compte le nombre de succès (ici le nombre de personnes recrutées) suit une loi
qui compte le nombre de succès (ici le nombre de personnes recrutées) suit une loi 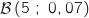 .
.
b. Calculer la probabilité que deux exactement des cinq amis soient recrutés. On arrondira à  qui compte le nombre de succès (ici le nombre de personnes recrutées) suit une loi
qui compte le nombre de succès (ici le nombre de personnes recrutées) suit une loi 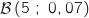 .
.
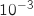 .
.
En utilisant la formule du cours on a directement :
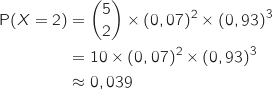
3. Quel est le nombre minimum de dossiers que le cabinet de recrutement doit traiter pour que la probabilité d'embaucher au moins un candidat soit supérieure à 0,999 ?
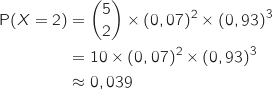
Soit  un entier naturel non nul qui représente le nombre de dossiers traités.
La variable aléatoire
un entier naturel non nul qui représente le nombre de dossiers traités.
La variable aléatoire 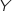 , qui compte le nombre de personnes recrutées suit une loi binomiale
, qui compte le nombre de personnes recrutées suit une loi binomiale 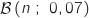 .
On s'intéresse à :
.
On s'intéresse à :
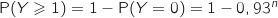 .
et il s'agit de résoudre :
.
et il s'agit de résoudre :
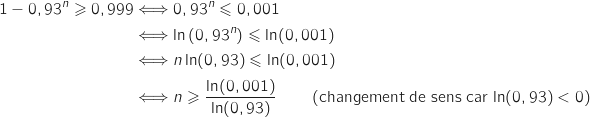 avec
avec 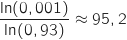 Donc il faut traiter au minimum 96 dossiers pour répondre au critère de probabilité demandé.
Donc il faut traiter au minimum 96 dossiers pour répondre au critère de probabilité demandé.
 un entier naturel non nul qui représente le nombre de dossiers traités.
La variable aléatoire
un entier naturel non nul qui représente le nombre de dossiers traités.
La variable aléatoire 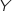 , qui compte le nombre de personnes recrutées suit une loi binomiale
, qui compte le nombre de personnes recrutées suit une loi binomiale 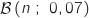 .
On s'intéresse à :
.
On s'intéresse à :
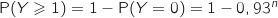 .
et il s'agit de résoudre :
.
et il s'agit de résoudre :
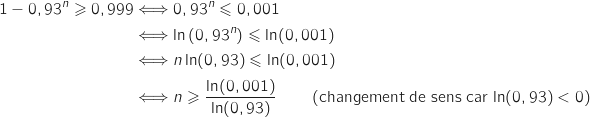 avec
avec 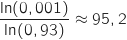 Donc il faut traiter au minimum 96 dossiers pour répondre au critère de probabilité demandé.
Donc il faut traiter au minimum 96 dossiers pour répondre au critère de probabilité demandé.
