Corrigé de l'exercice 3 du bac S de maths de juin 2012 en métropole
Cacher les corrigés
Partie A
On désigne par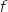 la fonction définie sur l'intervalle
la fonction définie sur l'intervalle 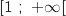 par
par
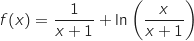
1. Déterminer la limite de la fonction
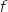 en
en 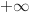 .
.
-
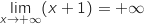 et par inverse
et par inverse 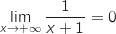 .
.
-
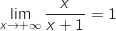 (termes de plus haut degré)
et par composée
(termes de plus haut degré)
et par composée 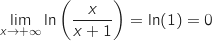 .
.
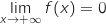 .
.
2. Démontrer que pour tout réel
 de l'intervalle
de l'intervalle 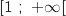 ,
, 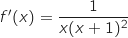 .
Dresser le tableau de variation de la fonction
.
Dresser le tableau de variation de la fonction 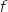 .
.
La fonction 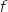 est dérivable sur
est dérivable sur 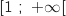 et on a :
et on a :
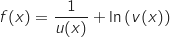 avec :
avec :
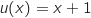
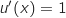
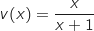
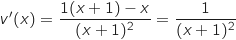 (formule du quotient)
Donc
(formule du quotient)
Donc  Pour tout
Pour tout 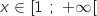 ,
, 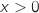 et
et 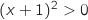 donc
donc 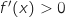 et on a le tableau de variations :
et on a le tableau de variations :
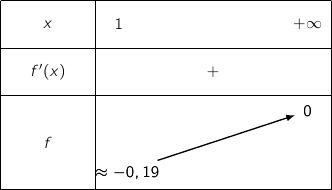
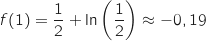 .
.
3. En déduire le signe de la fonction  est dérivable sur
est dérivable sur  et on a :
et on a :
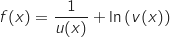 avec :
avec :
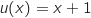
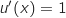
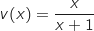
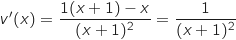 (formule du quotient)
Donc
(formule du quotient)
Donc  Pour tout
Pour tout 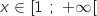 ,
, 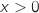 et
et 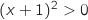 donc
donc 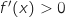 et on a le tableau de variations :
et on a le tableau de variations :

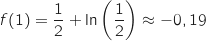 .
.
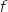 sur l'intervalle
sur l'intervalle 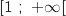 .
.
D'après l'étude précédente on a 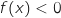 pour tout
pour tout 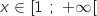 .
.
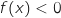 pour tout
pour tout 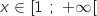 .
.
Partie B
Soit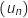 la suite définie pour tout entier strictement positif par
la suite définie pour tout entier strictement positif par
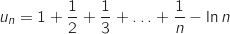

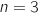 .
.
La boucle est executée 3 fois.
Itération 1 : 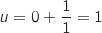 Itération 2 :
Itération 2 : 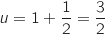 Itération 3 :
Itération 3 : 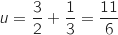 Donc la valeur exacte affichée est
Donc la valeur exacte affichée est 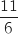 .
.
2. Recopier et compléter l'algorithme précédent afin qu'il affiche la valeur de 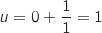 Itération 2 :
Itération 2 : 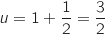 Itération 3 :
Itération 3 : 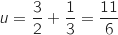 Donc la valeur exacte affichée est
Donc la valeur exacte affichée est 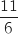 .
.
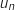 lorsque l'utilisateur entre la valeur de
lorsque l'utilisateur entre la valeur de  .
.

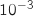 .
.
 A l'aide de ce tableau, formuler des conjectures sur le sens de variation de la suite
A l'aide de ce tableau, formuler des conjectures sur le sens de variation de la suite 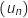 et son éventuelle convergence.
et son éventuelle convergence.
La suite semble décroissante et converger vers une valeur proche de 0,577.
Partie C
Cette partie permet de démontrer les conjectures formulées à propos de la suite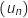 telle que pour tout entier strictement positif
telle que pour tout entier strictement positif  ,
,
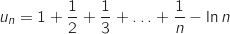
 ,
,
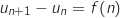
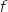 est la fonction définie dans la partie A.
En déduire le sens de variation de la suite
est la fonction définie dans la partie A.
En déduire le sens de variation de la suite 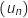 .
.
Pour tout entier 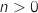 on a :
on a :
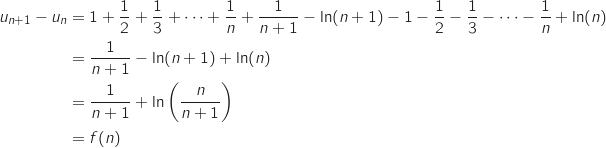 or pour tout
or pour tout 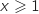 , on a vu que
, on a vu que 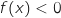 , donc pour tout entier
, donc pour tout entier 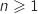 ,
, 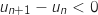 , ce qui prouve que la suite
, ce qui prouve que la suite 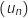 est strictement décroissante.
est strictement décroissante.
2.a. Soit 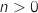 on a :
on a :
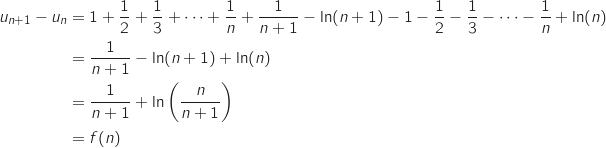 or pour tout
or pour tout 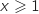 , on a vu que
, on a vu que 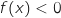 , donc pour tout entier
, donc pour tout entier 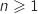 ,
, 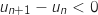 , ce qui prouve que la suite
, ce qui prouve que la suite 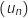 est strictement décroissante.
est strictement décroissante.
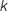 un entier strictement positif.
Justifier l'inégalité
un entier strictement positif.
Justifier l'inégalité 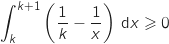 .
En déduire que
.
En déduire que 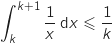 .
Démontrer l'inégalité
.
Démontrer l'inégalité 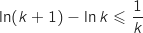 (1).
(1).
Soit 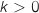 , pour tout
, pour tout 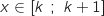 on a :
on a :
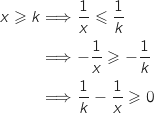 Du coup en intégrant cette fonction positive (avec la borne basse inférieure à la borne haute) on obtient
Du coup en intégrant cette fonction positive (avec la borne basse inférieure à la borne haute) on obtient 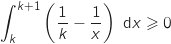 .
Par linéarité de l'intégrale en partant de l'inégalité qu'on vient de prouver on a :
.
Par linéarité de l'intégrale en partant de l'inégalité qu'on vient de prouver on a :
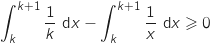 soit
soit 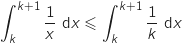 avec :
avec : 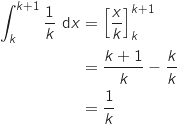 et donc on a bien :
et donc on a bien : 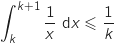 .
Pour terminer,
.
Pour terminer, 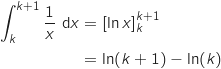 donc à partir de l'inégalité
donc à partir de l'inégalité 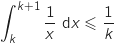 , on obtient
, on obtient 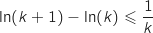 .
.
b. Ecrire l'inégalité (1) en remplaçant successivement 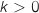 , pour tout
, pour tout 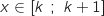 on a :
on a :
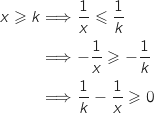 Du coup en intégrant cette fonction positive (avec la borne basse inférieure à la borne haute) on obtient
Du coup en intégrant cette fonction positive (avec la borne basse inférieure à la borne haute) on obtient 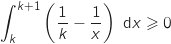 .
Par linéarité de l'intégrale en partant de l'inégalité qu'on vient de prouver on a :
.
Par linéarité de l'intégrale en partant de l'inégalité qu'on vient de prouver on a :
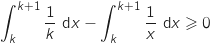 soit
soit 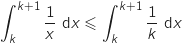 avec :
avec : 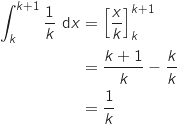 et donc on a bien :
et donc on a bien : 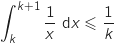 .
Pour terminer,
.
Pour terminer, 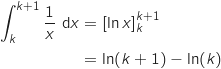 donc à partir de l'inégalité
donc à partir de l'inégalité 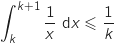 , on obtient
, on obtient 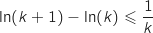 .
.
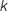 par 1, 2,
par 1, 2, 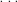 ,
,  et démontrer que pour tout entier strictement positif
et démontrer que pour tout entier strictement positif  ,
,
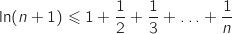
Pour tout entier 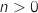 , on a les inégalités :
, on a les inégalités :
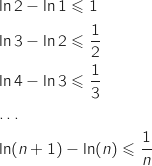 en ajoutant membre à membre ces inégalités on obtient :
en ajoutant membre à membre ces inégalités on obtient :
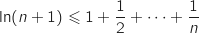 .
.
c. En déduire que pour tout entier strictement positif 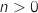 , on a les inégalités :
, on a les inégalités :
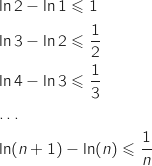 en ajoutant membre à membre ces inégalités on obtient :
en ajoutant membre à membre ces inégalités on obtient :
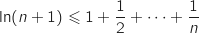 .
.
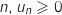 .
.
On remarque que 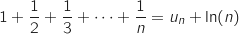 , donc en exploitant l'inégalité vue à la question précédente on a pour tout entier
, donc en exploitant l'inégalité vue à la question précédente on a pour tout entier 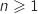 :
:
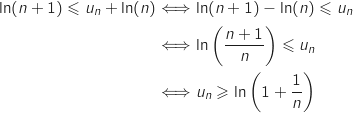 or pour tout entier
or pour tout entier 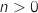 ,
, 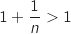 et
et 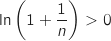 , donc on a aussi
, donc on a aussi 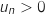 .
.
3. Prouver que la suite 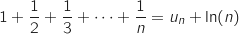 , donc en exploitant l'inégalité vue à la question précédente on a pour tout entier
, donc en exploitant l'inégalité vue à la question précédente on a pour tout entier 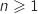 :
:
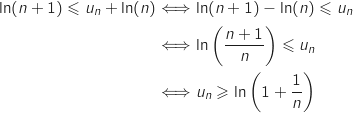 or pour tout entier
or pour tout entier 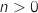 ,
, 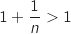 et
et 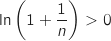 , donc on a aussi
, donc on a aussi 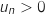 .
.
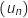 est convergente. On ne demande pas de calculer sa limite.
est convergente. On ne demande pas de calculer sa limite.
La suite 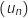 est décroissante et minorée par 0, donc elle est convergente.
est décroissante et minorée par 0, donc elle est convergente.
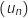 est décroissante et minorée par 0, donc elle est convergente.
est décroissante et minorée par 0, donc elle est convergente.
