Corrigé de l'exercice 4 du bac S de maths de juin 2012 en métropole
Cacher les corrigés
Cet exercice n'est pas dans l'esprit du nouveau programme en vigueur pour la session 2013. Cependant la première question
peut être encore réalisée par les élèves dans le seul but calculatoire.
Le plan complexe est muni d'un repère orthonormé direct 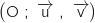 .
On appelle
.
On appelle  l'application qui à tout point
l'application qui à tout point 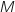 d'affixe
d'affixe  différente de
différente de 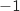 , fait correspondre le
point
, fait correspondre le
point 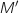 d'affixe
d'affixe 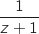 .
Le but de l'exercice est de déterminer l'image par
.
Le but de l'exercice est de déterminer l'image par  de la droite
de la droite  d'équation
d'équation 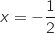 .
1. Soient A, B et C les points d'affixes respectives
.
1. Soient A, B et C les points d'affixes respectives
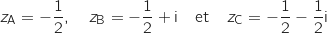
a. Placer les trois points A, B et C sur une figure que l'on fera sur la copie en prenant 2cm pour unité graphique.
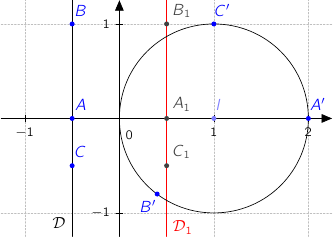
b. Calculer les affixes des points A
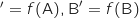 et C
et C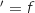 (C) et placer les points A', B'et C' sur la figure.
(C) et placer les points A', B'et C' sur la figure.
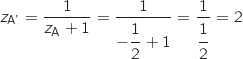
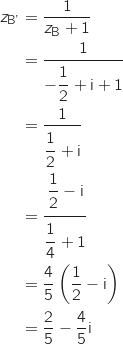
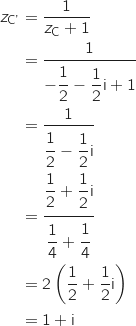
 , B
, B et C
et C ne sont pas alignés.
ne sont pas alignés.
On détermine, par exemple, les affixes des vecteurs 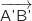 et
et 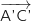 .
.
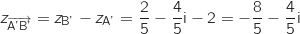
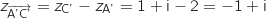 On remarque qu'il n'existe aucun réel
On remarque qu'il n'existe aucun réel  , tel que
, tel que 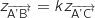 donc les vecteurs
donc les vecteurs
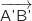 et
et 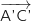 ne sont pas colinéaires et les points A', B' et C' ne sont pas alignés.
ne sont pas colinéaires et les points A', B' et C' ne sont pas alignés.
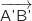 et
et 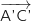 .
.
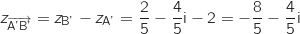
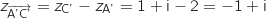 On remarque qu'il n'existe aucun réel
On remarque qu'il n'existe aucun réel  , tel que
, tel que 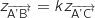 donc les vecteurs
donc les vecteurs
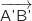 et
et 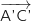 ne sont pas colinéaires et les points A', B' et C' ne sont pas alignés.
ne sont pas colinéaires et les points A', B' et C' ne sont pas alignés.
La fin de l'exercice original utilise des transformations du plan qui sont désormais hors programme.
