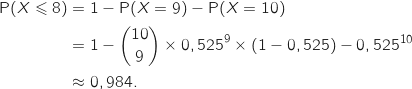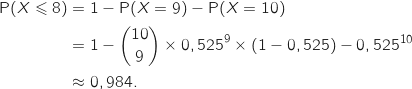Sujet et corrigé de l'exercice 1 du bac S de maths de juin 2013 en métropole
Cacher les corrigés
Une jardinerie vend de jeunes plants d'arbres qui proviennent de trois horticulteurs : 35 % des plants proviennent de l'horticulteur H
, 25 % de l'horticulteur H
et le reste de l'horticulteur H
.
Chaque horticulteur livre deux catégories d'arbres : des conifères et des arbres à feuilles.
La livraison de l'horticulteur H comporte 80 % de conifères alors que celle de l'horticulteur H n'en comporte que 50 % et celle de l'horticulteur H seulement 30 %.
1. Le gérant de la jardinerie choisit un arbre au hasard dans son stock. On envisage les événements suivants :
- H : « l'arbre choisi a été acheté chez l'horticulteur H »,
- H : « l'arbre choisi a été acheté chez l'horticulteur H »,
- H : « l'arbre choisi a été acheté chez l'horticulteur H »,
- C : « l'arbre choisi est un conifère »,
- F : « l'arbre choisi est un arbre feuillu ».
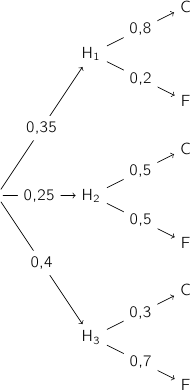
b. Calculer la probabilité que l'arbre choisi soit un conifère acheté chez l'horticulteur H
.
On utilise la formule des probabilités composées (multiplication des probabilités sur les branches de l'arbre) :
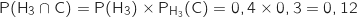
c. Justifier que la probabilité de l'évènement C est égale à 0,525.
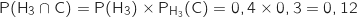
Les événements H
, H
et H
constituent un système complet d'événements donc
d'après la formule des probabilités totales on a :
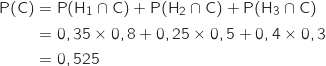
d. L'arbre choisi est un conifère.
Quelle est la probabilité qu'il ait été acheté chez l'horticulteur H, H et H constituent un système complet d'événements donc
d'après la formule des probabilités totales on a :
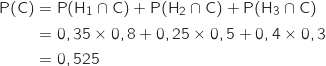
? On arrondira à 
.
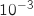On utilise la formule de calcul d'une probabilité conditionnelle :
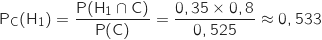
2. On choisit au hasard un échantillon de 10 arbres dans le stock de cette jardinerie.
On suppose que ce stock est suffisamment important pour que ce choix puisse être assimilé à un tirage avec remise de 10 arbres dans le stock.
On appelle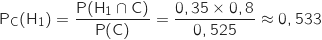
la variable aléatoire qui donne le nombre de conifères de l'échantillon choisi.
a. Justifier que suit une loi binomiale dont on précisera les paramètres.
On répète 10 fois de façon indépendante (le tirage est considéré avec remise), une même
expérience de Bernoulli dont la probabilité du succès (l'arbre est un conifère) vaut 0,525.
Donc la variable aléatoire qui compte le nombre de succès suit une loi binomiale dont
les paramètres son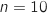t 
et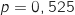 
.
b. Quelle est la probabilité que l'échantillon prélevé comporte exactement 5 conifères ?
On arrondira à qui compte le nombre de succès suit une loi binomiale dont
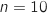les paramètres sont et .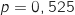
.
.
.
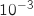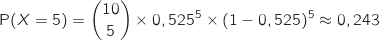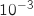Il faut bien comprendre que l'événement « au moins deux feuillus » correspond à
l'événement « au plus 8 conifères » et du coup on calcule :
