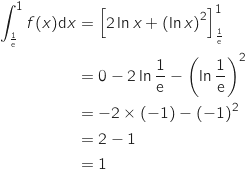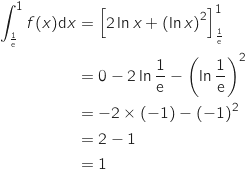Sujet et corrigé de l'exercice 2 du bac S de maths de juin 2013 en métropole
Cacher les corrigés
Sur le graphique ci-dessous, on a tracé, dans le plan muni d'un repère orthonormé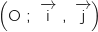 ,
la courbe représentative
,
la courbe représentative  d'une fonction
d'une fonction  définie et dérivable sur l'intervalle
définie et dérivable sur l'intervalle  .
.
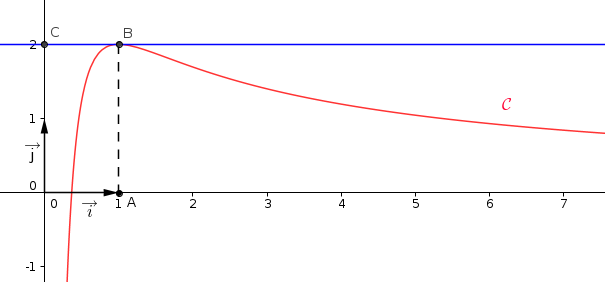
On dispose des informations suivantes :
- les points A, B, C ont pour coordonnées respectives
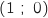 ,
, 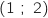 ,
, 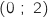 ;
;
- la courbe
 passe par le point B et la droite (BC) est tangente à
passe par le point B et la droite (BC) est tangente à  en B ;
en B ;
- il existe deux réels positifs
 et
et  tels que pour tout réel strictement positif
tels que pour tout réel strictement positif  ,
,
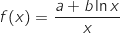
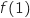 et
et 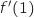 .
.
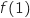 est l'ordonnée de B, donc
est l'ordonnée de B, donc 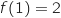 .
.
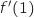 est le coefficient directeur de (BC), or B et C ont même ordonnée, donc le coefficient directeur de cette droite vaut 0 et du coup
est le coefficient directeur de (BC), or B et C ont même ordonnée, donc le coefficient directeur de cette droite vaut 0 et du coup 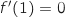 .
.
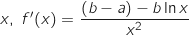 .
.
On peut écrire 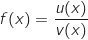 avec :
avec :
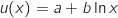 ;
; 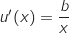
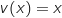 ;
; 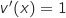 .
En utilisant la formule de la dérivée d'un quotient il vient :
.
En utilisant la formule de la dérivée d'un quotient il vient :
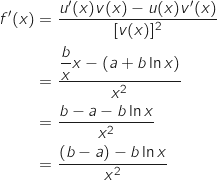
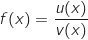 avec :
avec :
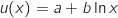 ;
; 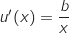
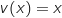 ;
; 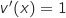 .
En utilisant la formule de la dérivée d'un quotient il vient :
.
En utilisant la formule de la dérivée d'un quotient il vient :
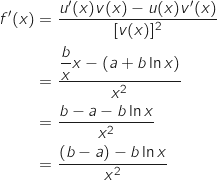
c. En déduire les réels
 et
et  .
.
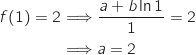
 Donc
Donc 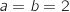 et
et 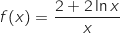 .
.
 appartenant à l'intervalle
appartenant à l'intervalle  ,
,  a le même signe que
a le même signe que 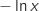 .
.
En remplaçant  et
et  par 2 dans la formule de la question 1.b. on a :
par 2 dans la formule de la question 1.b. on a :
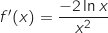 Pour tout
Pour tout 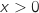 ;
; 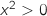 et donc
et donc  est du même signe que
est du même signe que 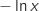 .
.
b. Déterminer les limites de  et
et  par 2 dans la formule de la question 1.b. on a :
par 2 dans la formule de la question 1.b. on a :
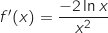 Pour tout
Pour tout 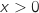 ;
; 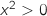 et donc
et donc  est du même signe que
est du même signe que 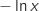 .
.
 en 0 et en
en 0 et en  . On pourra remarquer que pour tout réel
. On pourra remarquer que pour tout réel
 strictement positif,
strictement positif, 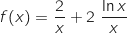 .
.
Limite à droite en 0
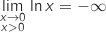 et donc
et donc 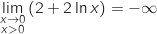 .
.
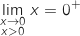 Finalement, par quotient,
Finalement, par quotient, 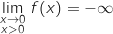 .
Limite en
.
Limite en  On a une forme indéterminée, on utilise l'écriture :
On a une forme indéterminée, on utilise l'écriture : 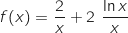 .
.
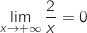
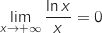 (limite connue vue en cours)
et donc
(limite connue vue en cours)
et donc 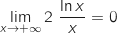 .
Finalement, par somme :
.
Finalement, par somme : 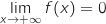 .
.
c. En déduire le tableau de variations de la fonction 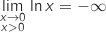 et donc
et donc 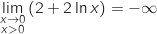 .
.
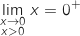 Finalement, par quotient,
Finalement, par quotient, 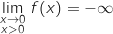 .
Limite en
.
Limite en  On a une forme indéterminée, on utilise l'écriture :
On a une forme indéterminée, on utilise l'écriture : 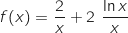 .
.
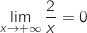
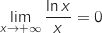 (limite connue vue en cours)
et donc
(limite connue vue en cours)
et donc 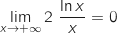 .
Finalement, par somme :
.
Finalement, par somme : 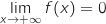 .
.
 .
.
En exploitant tous les éléments vu avant on peut dresser le tableau de variations complet
de la fonction.
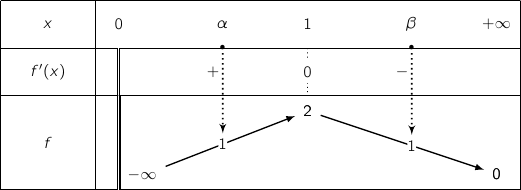
3.a. Démontrer que l'équation 
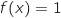 admet une unique solution
admet une unique solution  sur l'intervalle
sur l'intervalle 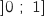 .
.
La fonction  est continue et strictement croissante sur
est continue et strictement croissante sur 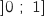 avec :
avec :
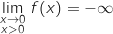 et
et 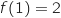 .
Comme
.
Comme 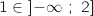 , on peut dire d'après le théorème des valeurs
intermédiaires que l'équation
, on peut dire d'après le théorème des valeurs
intermédiaires que l'équation 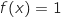 admet une unique solution
admet une unique solution  située dans
l'intervalle
située dans
l'intervalle 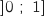 .
.
b. Par un raisonnement analogue, on démontre qu'il existe un unique réel  est continue et strictement croissante sur
est continue et strictement croissante sur 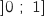 avec :
avec :
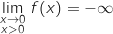 et
et 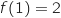 .
Comme
.
Comme 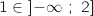 , on peut dire d'après le théorème des valeurs
intermédiaires que l'équation
, on peut dire d'après le théorème des valeurs
intermédiaires que l'équation 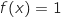 admet une unique solution
admet une unique solution  située dans
l'intervalle
située dans
l'intervalle 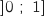 .
.
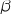 de l'intervalle
de l'intervalle 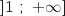 tel que
tel que 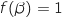 .
Déterminer l'entier
.
Déterminer l'entier  tel que
tel que 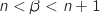 .
.
En utilisant la calculette, par balayage on trouve facilement : 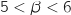 , donc
, donc 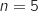 .
.
4. On donne l'algorithme ci-dessous.
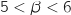 , donc
, donc 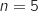 .
.

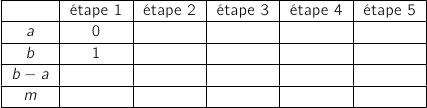
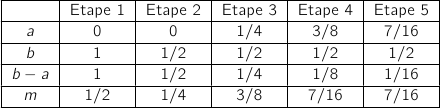
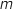 n'est pas modifiée.
n'est pas modifiée.
Les valeurs affichées sont les bornes d'un encadrement de  d'amplitude
d'amplitude 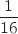 .
.
c. Modifier l'algorithme ci-dessus pour qu'il affiche les deux bornes d'un encadrement de  d'amplitude
d'amplitude 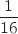 .
.
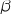 d'amplitude
d'amplitude 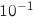 .
.
On a vu que 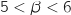 , donc on initialise
, donc on initialise  et
et  avec ces valeurs.
Sur
avec ces valeurs.
Sur 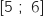 , la fonction
, la fonction  est décroissante, donc au niveau du traitement il
faut modifier « Si
est décroissante, donc au niveau du traitement il
faut modifier « Si 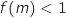 » en « Si
» en « Si 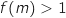 ».
L'algorithme ainsi obtenu est le suivant :
».
L'algorithme ainsi obtenu est le suivant :

On pourra remarquer que l'algorithme ainsi modifié ne donne pas exactement un encadrement
d'amplitude 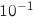 , mais un encadrement d'amplitude inférieure ou égale à
, mais un encadrement d'amplitude inférieure ou égale à 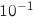 .
.
5. Le but de cette question est de démontrer que la courbe 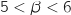 , donc on initialise
, donc on initialise  et
et  avec ces valeurs.
Sur
avec ces valeurs.
Sur 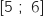 , la fonction
, la fonction  est décroissante, donc au niveau du traitement il
faut modifier « Si
est décroissante, donc au niveau du traitement il
faut modifier « Si 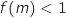 » en « Si
» en « Si 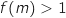 ».
L'algorithme ainsi obtenu est le suivant :
».
L'algorithme ainsi obtenu est le suivant :

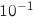 , mais un encadrement d'amplitude inférieure ou égale à
, mais un encadrement d'amplitude inférieure ou égale à 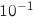 .
.
 partage le rectangle OABC en deux domaines d'aires égales.
a. Justifier que cela revient à démontrer que
partage le rectangle OABC en deux domaines d'aires égales.
a. Justifier que cela revient à démontrer que 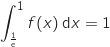 .
.
On commence par déterminer l'abscisse du point d'intersection de  avec l'axe
des abscisses, pour cela on résout :
avec l'axe
des abscisses, pour cela on résout :
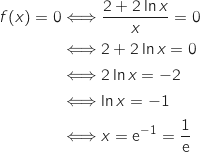 On remarque que sur
On remarque que sur 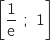 , la fonction
, la fonction  est positive
et donc l'aire du domaine délimité par
est positive
et donc l'aire du domaine délimité par  , l'axe des abscisses et la droite
d'équation
, l'axe des abscisses et la droite
d'équation  est égal à
est égal à 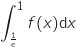 .
Ce domaine est un des deux domaines qui partage le rectangle OABC, le rectangle
ayant une aire de 2 u.a., on doit donc montrer que
.
Ce domaine est un des deux domaines qui partage le rectangle OABC, le rectangle
ayant une aire de 2 u.a., on doit donc montrer que 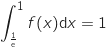
b. En remarquant que l'expression de  avec l'axe
des abscisses, pour cela on résout :
avec l'axe
des abscisses, pour cela on résout :
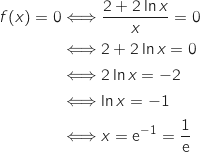 On remarque que sur
On remarque que sur 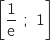 , la fonction
, la fonction  est positive
et donc l'aire du domaine délimité par
est positive
et donc l'aire du domaine délimité par  , l'axe des abscisses et la droite
d'équation
, l'axe des abscisses et la droite
d'équation  est égal à
est égal à 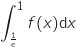 .
Ce domaine est un des deux domaines qui partage le rectangle OABC, le rectangle
ayant une aire de 2 u.a., on doit donc montrer que
.
Ce domaine est un des deux domaines qui partage le rectangle OABC, le rectangle
ayant une aire de 2 u.a., on doit donc montrer que 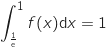
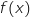 peut s'écrire
peut s'écrire 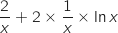 , terminer la démonstration.
, terminer la démonstration.
Il s'agit maintenant de calculer la valeur exacte de l'intégrale précédente :