Sujet et corrigé de l'exercice 3 du bac S de maths de juin 2013 en métropole
Cacher les corrigés
Pour chacune des propositions suivantes, indiquer si elle est vraie ou fausse et justifier la réponse choisie. Il est attribué un point par réponse exacte correctement justifiée. Une réponse non justifiée n'est pas prise en compte. Une absence de réponse n'est pas pénalisée.
1. Proposition 1 : Dans le plan muni d'un repère orthonormé, l'ensemble des points
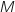dont l'affixe 
vérifie l'égalité 
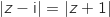est une droite.
Considérons le point A d'affixe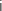 
et le point B d'affixe 
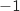, alors on a :
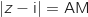et 
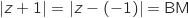Du coup l'égalité proposée équivaut à 
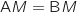et donc l'ensemble des points 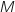considéré est la médiatrice de [AB], c'est bien une droite.
L'affirmation est VRAIE.
2. Proposition 2 : Le nombre complexe 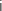et le point B d'affixe 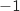, alors on a :
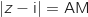et
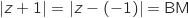Du coup l'égalité proposée équivaut à 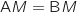et donc l'ensemble des points 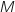considéré est la médiatrice de [AB], c'est bien une droite.
L'affirmation est VRAIE.
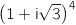est un nombre réel.
Travaillons déjà avec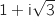 
.
Le module de ce nombre complexe est 
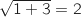et donc on peut écrire :
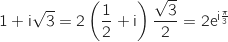Du coup on a :
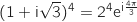Comme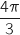 
n'est pas un multiple de 
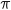, le nombre en question n'est pas un réel.
L'affirmation est FAUSSE.
.
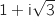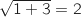Le module de ce nombre complexe est et donc on peut écrire :
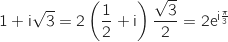Du coup on a :
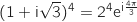Comme 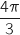n'est pas un multiple d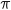e , le nombre en question n'est pas un réel.
L'affirmation est FAUSSE.
3. Soit ABCDEFGH un cube.
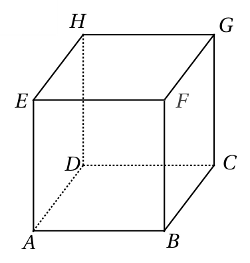
On peut se placer, par exemple, dans le repère orthonormé
.
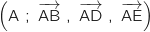Dans ce repère on a : 
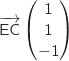et
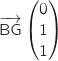On calcule le produit scalaire :
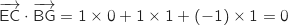Cela montre que 
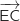et 
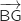sont orthogonaux.
L'affirmation est VRAIE.
4. L'espace est muni d'un repère orthonormé .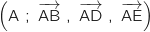
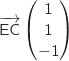Dans ce repère on a : et
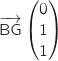On calcule le produit scalaire :
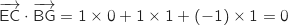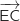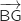Cela montre que et sont orthogonaux.
L'affirmation est VRAIE.
.
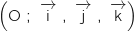Soit le plan 
d'équation cartésienne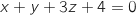 
.
On note S le point de coordonnées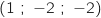 
.
Proposition 4 : La droite qui passe par S et qui est perpendiculaire au plan a pour représentation paramétrique
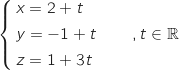
Par lecture sur les équations données on a directement :
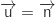, la droite en question est
bien orthogonale au plan. Il reste à vérifier que S appartient à la droite.
S appartient à la droite équivaut à :
.
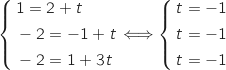Donc c'est bon !
L'affirmation est VRAIE.
- un vecteur normal de :
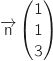
- un vecteur directeur de la droite :
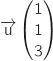
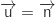, la droite en question est
bien orthogonale au plan. Il reste à vérifier que S appartient à la droite.
S appartient à la droite équivaut à :
.
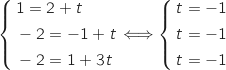Donc c'est bon !
L'affirmation est VRAIE.
