Sujet et corrigé de l'exercice 4 du bac S de maths de juin 2013 en métropole
Cacher les corrigés
Soit la suite numérique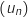 définie sur
définie sur 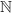 par :
par :
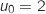 et pour tout entier naturel
et pour tout entier naturel  ,
,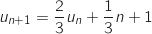
1.a. Calculer
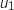 ,
, 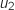 ,
, 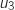 et
et 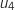 .
On pourra en donner des valeurs approchées à
.
On pourra en donner des valeurs approchées à 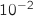 près.
près.
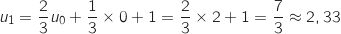
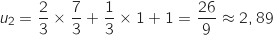
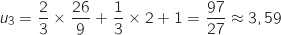
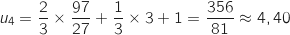
Il semble que la suite soit croissante.
2.a. Démontrer que pour tout entier naturel
 ,
,
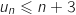
On démontre par récurrence la propriété :
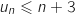
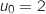 et
et 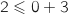 donc
donc 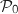 est vraie.
Hérédité
On suppose qu'à un rang
est vraie.
Hérédité
On suppose qu'à un rang  ,
, 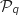 est vraie, soit
est vraie, soit 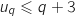 .
On part de cette hypothèse :
.
On part de cette hypothèse :
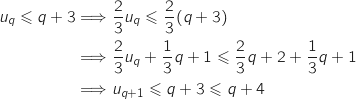 Donc
Donc  est vraie, ce qui montre l'hérédité.
Ainsi la propriété en question est initialisée au rang 0 et elle est héréditaire donc
elle est vraie pour tout entier naturel.
est vraie, ce qui montre l'hérédité.
Ainsi la propriété en question est initialisée au rang 0 et elle est héréditaire donc
elle est vraie pour tout entier naturel.
b. Démontrer que pour tout entier naturel 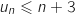
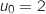 et
et 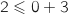 donc
donc 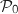 est vraie.
Hérédité
On suppose qu'à un rang
est vraie.
Hérédité
On suppose qu'à un rang  ,
, 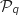 est vraie, soit
est vraie, soit 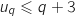 .
On part de cette hypothèse :
.
On part de cette hypothèse :
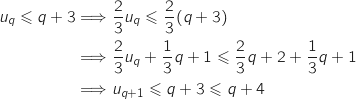 Donc
Donc  est vraie, ce qui montre l'hérédité.
Ainsi la propriété en question est initialisée au rang 0 et elle est héréditaire donc
elle est vraie pour tout entier naturel.
est vraie, ce qui montre l'hérédité.
Ainsi la propriété en question est initialisée au rang 0 et elle est héréditaire donc
elle est vraie pour tout entier naturel.
 ,
,
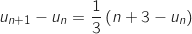
Pour tout entier naturel  , on a :
, on a :
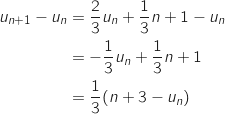
c. En déduire une validation de la conjecture précédente.
 , on a :
, on a :
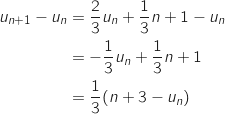
D'après la question a., 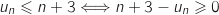 .
Du coup
.
Du coup 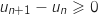 ce qui montre que la suite est croissante.
ce qui montre que la suite est croissante.
3. On désigne par 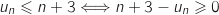 .
Du coup
.
Du coup 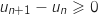 ce qui montre que la suite est croissante.
ce qui montre que la suite est croissante.
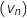 la suite définie sur
la suite définie sur 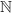 par
par 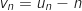 .
a. Démontrer que la suite
.
a. Démontrer que la suite 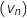 est une suite géométrique de raison
est une suite géométrique de raison  .
.
Pour tout entier naturel  on a :
on a :
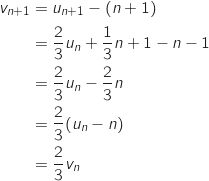 Cela prouve que la suite
Cela prouve que la suite  est une suite géométrique de raison
est une suite géométrique de raison  .
.
b. En déduire que pour tout entier naturel  on a :
on a :
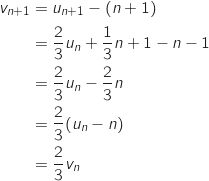 Cela prouve que la suite
Cela prouve que la suite  est une suite géométrique de raison
est une suite géométrique de raison  .
.
 ,
,
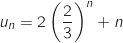
On a 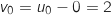 et donc
et donc 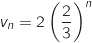 .
De plus :
.
De plus : 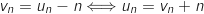 , en remplaçant
, en remplaçant 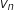 par sa formule
explicite il vient :
par sa formule
explicite il vient :
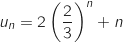
c. Déterminer la limite de la suite 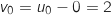 et donc
et donc 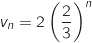 .
De plus :
.
De plus : 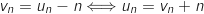 , en remplaçant
, en remplaçant 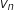 par sa formule
explicite il vient :
par sa formule
explicite il vient :
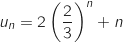
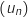 .
.
On a 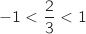 , donc
, donc 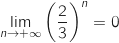 .
Par somme,
.
Par somme, 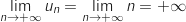 .
.
4. Pour tout entier naturel non nul 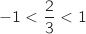 , donc
, donc 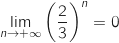 .
Par somme,
.
Par somme, 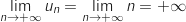 .
.
 , on pose:
, on pose:
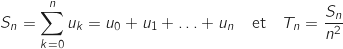
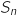 en fonction de
en fonction de  .
.
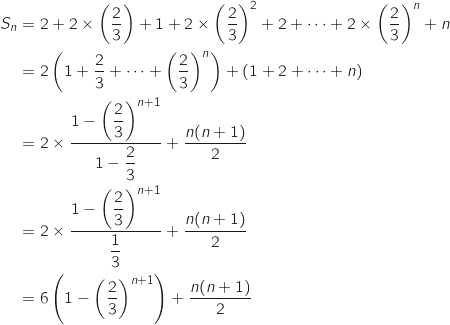
 .
.
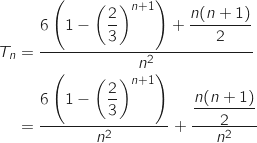
-
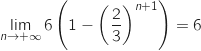 car
car 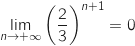 puisque
puisque 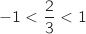 .
.
-
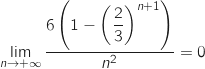
- Pour
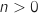 ,
, 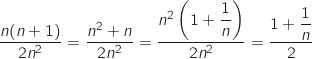
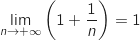 et
et
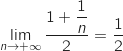
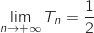 .
.
