Sujet et corrigé de l'exercice de spécialité du bac S de maths de juin 2013 en métropole
Cacher les corrigés
On étudie la population d'une région imaginaire. Le 1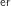 janvier 2013, cette région comptait 250 000 habitants dont 70 % résidaient à la campagne et 30 % en ville.
L'examen des données statistiques recueillies au cours de plusieurs années amène à choisir de modéliser l'évolution de la population pour les années à venir de la façon suivante :
janvier 2013, cette région comptait 250 000 habitants dont 70 % résidaient à la campagne et 30 % en ville.
L'examen des données statistiques recueillies au cours de plusieurs années amène à choisir de modéliser l'évolution de la population pour les années à venir de la façon suivante :
- l'effectif de la population est globalement constant,
- chaque année, 5 % de ceux qui résident en ville décident d'aller s'installer à la campagne et 1 % de ceux qui résident à la campagne choisissent d'aller habiter en ville.
 , on note
, on note 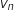 le nombre d'habitants de cette région qui résident en ville au 1
le nombre d'habitants de cette région qui résident en ville au 1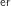 janvier de l'année
janvier de l'année 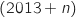 et
et
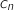 le nombre de ceux qui habitent à la campagne à la même date.
le nombre de ceux qui habitent à la campagne à la même date.
1. Pour tout entier naturel
 , exprimer
, exprimer 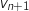 et
et 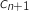 en fonction de
en fonction de 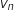 et
et 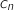 .
.
D'après les éléments de l'énoncé on a :
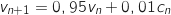
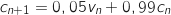
2. Soit la matrice 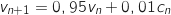
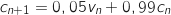
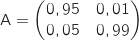 .
On pose
.
On pose 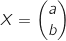 où
où  ,
,  sont deux réels fixés et
sont deux réels fixés et 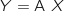 .
Déterminer, en fonction de
.
Déterminer, en fonction de  et
et  , les réels
, les réels  et
et 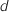 tels que
tels que 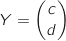 .
.
On calcule le produit :
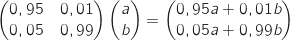 Donc
Donc 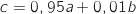 et
et 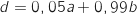
Les résultats précédents permettent d'écrire que pour tout entier naturel 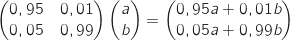 Donc
Donc 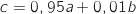 et
et 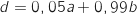
 ,
, 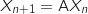 où
où 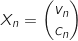 .
On peut donc en déduire que pour tout entier naturel
.
On peut donc en déduire que pour tout entier naturel  ,
, 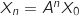 .
.
3. Soient les matrices
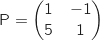 et
et 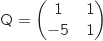 .
a. Calculer
.
a. Calculer 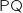 et
et 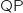 . En déduire la matrice
. En déduire la matrice 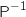 en fonction de Q.
en fonction de Q.
On a :
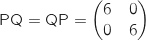 .
.
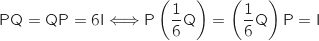 Du coup
Du coup 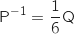 .
.
b. Vérifier que la matrice 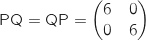 .
.
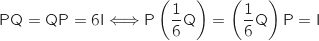 Du coup
Du coup 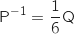 .
.
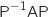 est une matrice diagonale D que l'on précisera.
est une matrice diagonale D que l'on précisera.
On calcule déja :
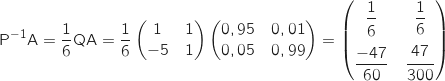 puis :
puis :
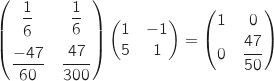
c. Démontrer que pour tout entier naturel 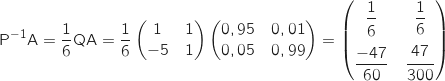 puis :
puis :
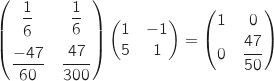
 supérieur ou égal à
supérieur ou égal à 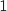 ,
, 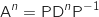 .
.
La propriété à montrer par récurrence pour tout entier  est :
est :
 : «
: « 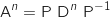 ».
Initialisation au rang 1
On sait que
».
Initialisation au rang 1
On sait que 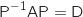 donc :
donc :
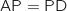 en mutipliant à gauche par
en mutipliant à gauche par 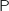 , puis :
, puis :
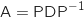 en multipliant à droite par
en multipliant à droite par 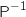 donc
donc 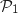 est vraie.
Hérédité
On suppose que
est vraie.
Hérédité
On suppose que 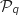 est vraie avec
est vraie avec 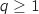 c'est à dire qu'on a l'hypothèse de récurrence :
c'est à dire qu'on a l'hypothèse de récurrence :
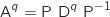
 est également vraie.
est également vraie.
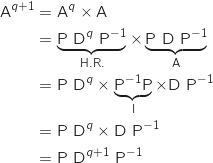 Donc
Donc  est vraie.
Ainsi la propriété
est vraie.
Ainsi la propriété  est vraie au rang 1 et est héréditaire donc elle est vraie pour tout entier naturel
est vraie au rang 1 et est héréditaire donc elle est vraie pour tout entier naturel 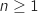 .
.
4. Les résultats des questions précédentes permettent d'établir que
 est :
est :
 : «
: « 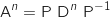 ».
Initialisation au rang 1
On sait que
».
Initialisation au rang 1
On sait que 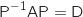 donc :
donc :
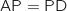 en mutipliant à gauche par
en mutipliant à gauche par 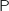 , puis :
, puis :
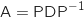 en multipliant à droite par
en multipliant à droite par 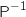 donc
donc 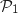 est vraie.
Hérédité
On suppose que
est vraie.
Hérédité
On suppose que 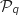 est vraie avec
est vraie avec 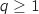 c'est à dire qu'on a l'hypothèse de récurrence :
c'est à dire qu'on a l'hypothèse de récurrence :
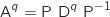
 est également vraie.
est également vraie.
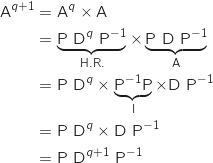 Donc
Donc  est vraie.
Ainsi la propriété
est vraie.
Ainsi la propriété  est vraie au rang 1 et est héréditaire donc elle est vraie pour tout entier naturel
est vraie au rang 1 et est héréditaire donc elle est vraie pour tout entier naturel 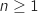 .
.
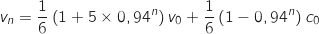
On détermine la limite de 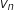 en
en  :
Comme
:
Comme 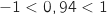 ,
, 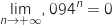 .
Du coup
.
Du coup 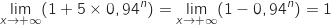 et :
et :
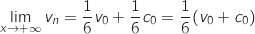 .
Cela signifie qu'à long terme
.
Cela signifie qu'à long terme  de la population va résider en ville et
de la population va résider en ville et  sera à la
campagne.
sera à la
campagne.
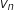 en
en  :
Comme
:
Comme 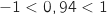 ,
, 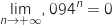 .
Du coup
.
Du coup 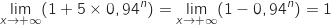 et :
et :
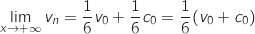 .
Cela signifie qu'à long terme
.
Cela signifie qu'à long terme  de la population va résider en ville et
de la population va résider en ville et  sera à la
campagne.
sera à la
campagne.
