Corrigé de l'exercice 1 de maths du bac S de mars 2012 en Nouvelle Calédonie
Cacher les corrigés
Partie A
On considère le polynôme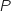
défini sur 
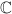par
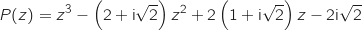
1. Montrer que le nombre complexe
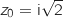est solution de l'équation 
.
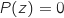On remplace 
dans l'expression 
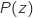et on vérifie en effectuant le calcul qu'on obtient 0.
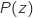2.a. Déterminer les réels dans l'expression et on vérifie en effectuant le calcul qu'on obtient 0.
et 
tels que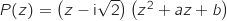 
.
On développe l'expression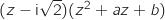 
ce qui donne :
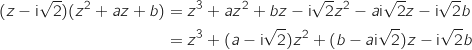Par identification on obtient :
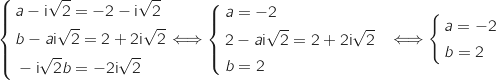Donc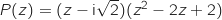 
b. En déduire les solutions dans 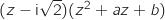ce qui donne :
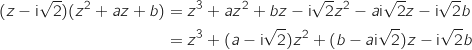Par identification on obtient :
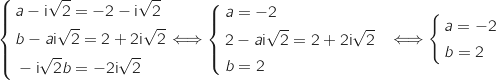Donc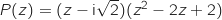
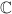de l'équation .
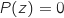On résout dans 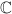l'équation 
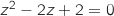, on trouve deux solutions complexes conjuguées qui sont 
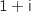et 
.
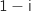Ainsi l'équation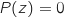 
admet trois solutions : 
, 
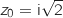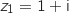et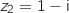 
.
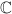l'équation 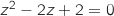, on trouve deux solutions complexes conjuguées qui sont 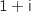et .
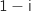Ainsi l'équation 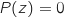admet trois solutions : 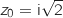, 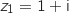et .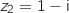
Partie B
Le plan complexe est muni d'un repère orthonormé direct \Ouv. On prendra 2 cm pour unité graphique. On considère les points A, B, J et K d'affixes respectives :
.
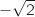Dans le sujet original il faut déterminer l'affixe de L en utilisant un transformation.
A partir de la rentrée 2012, les transformations en écriture complexe ne sont plus au programme.
3. Montrer que les points A, B, J et L appartiennent à un même cercle dont on précisera le centre et le rayon.
On conjecture que A, B, J et L sont sur le cercle de centre O et de rayon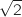 
.
Pour le vérifier on calcule les modules des affixes des points correspondants.
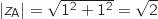
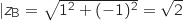
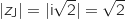
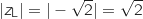
4. Soit D le point d'affixe .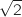
Pour le vérifier on calcule les modules des affixes des points correspondants.
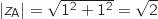
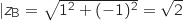
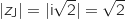
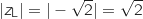
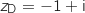et
C le point d'affixe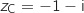 
.
Le contenu de cette question a été supprimé car dans le sujet original il fait intervenir des transformations.
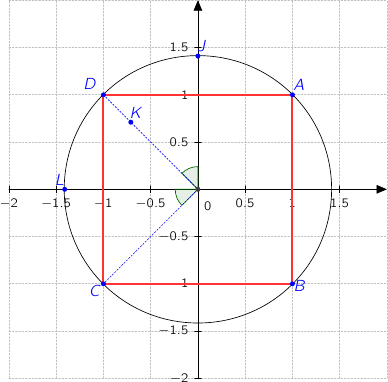
5. Quelle est la nature du quadrilatère ABCD ? Justifier la réponse.
On conjecture que ABCD est un carré.
.
.
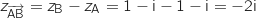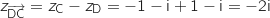Donc 
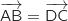, ce qui prouve que ABCD est un parallélogramme.
On s'intéresse maintenant aux vecteurs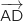 
et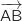 
.
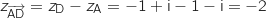
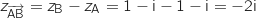On a donc 
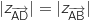et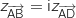 
, ce qui prouve que les côtés consécutifs [AD] et [AB] du parallélogramme ABCD sont de même longueur et perpendiculaires, donc ABCD est un carré.
.
.
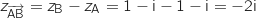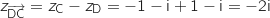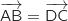Donc , ce qui prouve que ABCD est un parallélogramme.
On s'intéresse maintenant aux vecteurs 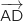et .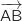
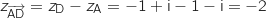
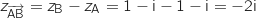On a donc 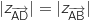et 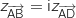, ce qui prouve que les côtés consécutifs [AD] et [AB] du parallélogramme ABCD sont de même longueur et perpendiculaires, donc ABCD est un carré.
