Corrigé de l'exercice 3 de maths du bac S de mars 2012 en Nouvelle Calédonie
Cacher les corrigés
Pour chacun des énoncés suivants, indiquer si la proposition correspondante est vraie ou fausse et proposer une justification de la réponse choisie. Enoncé 1 : Soit
une suite non constante de réels.
Pour tout entier 
, on pose 
.
Proposition 1
« On peut choisir la suite telle que la suite 
converge vers 
. »
VRAI.
Il suffit de prendre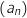 
telle que 
et dans ce cas par continuité de la fonction 
on aura
.
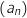telle que et dans ce cas par continuité de la fonction on aura
.
Enoncé 2 : Dans le plan complexe d'origine O, on considère, pour tout entier naturel non nul
, les points 
d'affixe 
.
Proposition 2
« Les points O, 
et 
sont alignés. »
FAUX.
Une mesure de l'angle 
est donnée par un argument de 
avec 
.
Donc 
et 
.
Ce n'est ni un angle plat, ni un angle nul donc O; M
et M
ne sont pas alignés.
est donnée par un argument de avec .
Donc et .
Ce n'est ni un angle plat, ni un angle nul donc O; M et M ne sont pas alignés.
Enoncé 3 : On considère une fonction
, sa dérivée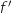 
et son unique primitive 
s'annulant en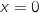 
. Les représentations graphiques de ces trois fonctions sont données (dans le désordre) par les courbes ci-dessous.
Proposition 3
« La courbe 
ci-dessous est la représentation graphique de . »
Courbe 2
Courbe 3
FAUX.
Si la courbe 3 est celle de , alors la primitive s'annulant en 0 ne peut être représentée que par la courbe 1 et du coup la courbe 2 est celle de .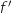
Il reste à voir si cela est cohérent.
En observant la courbe 2 et la courbe 3 on ne voit aucune incohérence : le signe de la dérivée sur la courbe 2 est cohérent avec les variations de la fonction sur la courbe 3.
En revanche en observant les courbes 1 et 3 on constate des incohérences, par exemple, sur 
, la fonction (courbe 1) est croissante alors
que la fonction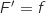 
(courbe 3) est négative.
, alors la primitive s'annulant en 0 ne peut être représentée que par la courbe 1 et du coup la courbe 2 est celle de .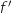
Il reste à voir si cela est cohérent.
En observant la courbe 2 et la courbe 3 on ne voit aucune incohérence : le signe de la dérivée sur la courbe 2 est cohérent avec les variations de la fonction sur la courbe 3.
En revanche en observant les courbes 1 et 3 on constate des incohérences, par exemple, sur , la fonction (courbe 1) est croissante alors
que la fonction 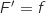(courbe 3) est négative.
Dans le sujet original la fin de l'exercice aborde des notions qui ne sont plus au programme à compter de la
session 2013 du baccalauréat.
