Corrigé de l'exercice 4 de maths du bac S de mars 2012 en Nouvelle Calédonie
Cacher les corrigés
Soit la fonction définie sur
la fonction définie sur  par
par 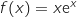 .
On désigne par
.
On désigne par  la courbe représentative de
la courbe représentative de  dans le plan muni d'un repère orthogonal
dans le plan muni d'un repère orthogonal 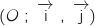 .
Soit
.
Soit  un nombre réel appartenant à l'intervalle
un nombre réel appartenant à l'intervalle  .
Sur la courbe
.
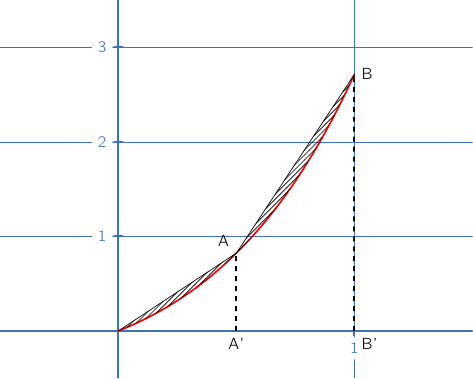
Sur la courbe  , tracée ci-dessous, on a placé les points A et B d'abscisses respectives
, tracée ci-dessous, on a placé les points A et B d'abscisses respectives  et
et 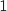 . On a tracé les segments [OA] et [AB]. On a hachuré la partie du plan délimitée par les segments [OA] et [AB] et la courbe
. On a tracé les segments [OA] et [AB]. On a hachuré la partie du plan délimitée par les segments [OA] et [AB] et la courbe  . On a placé les points A
. On a placé les points A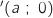 et B
et B .
Le but de l'exercice est de déterminer la valeur du nombre réel
.
Le but de l'exercice est de déterminer la valeur du nombre réel  pour laquelle l'aire de la partie du plan hachurée est minimale.
pour laquelle l'aire de la partie du plan hachurée est minimale.
PARTIE A
1. On admet que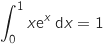 .
.
Dans le sujet original il faut calculer cette intégrale ce qui nécessite l'utilisation d'une intégration par parties.
Cette méthode d'intégration n'est plus au programmme à partir de l'année scolaire 2012-2013.
2.a. Donner l'aire du triangle OAA et montrer que l'aire du trapèze ABB
et montrer que l'aire du trapèze ABB A
A est égale à
est égale à 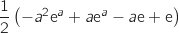 .
.
On a A'A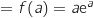 et OA'
et OA'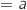 donc l'aire de OAA' vaut :
donc l'aire de OAA' vaut :
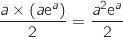 .
Pour l'aire du trapèze on a les bases qui mesurent :
AA'
.
Pour l'aire du trapèze on a les bases qui mesurent :
AA'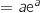 et BB'
et BB'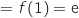 .
La hauteur mesure : OB'
.
La hauteur mesure : OB' OA'
OA'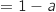 , d'où l'aire du trapèze :
, d'où l'aire du trapèze :
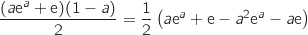 .
.
b. En déduire que l'aire de la partie du plan hachurée est égale à 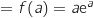 et OA'
et OA'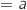 donc l'aire de OAA' vaut :
donc l'aire de OAA' vaut :
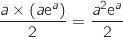 .
Pour l'aire du trapèze on a les bases qui mesurent :
AA'
.
Pour l'aire du trapèze on a les bases qui mesurent :
AA'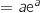 et BB'
et BB'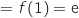 .
La hauteur mesure : OB'
.
La hauteur mesure : OB' OA'
OA'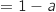 , d'où l'aire du trapèze :
, d'où l'aire du trapèze :
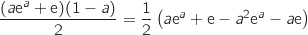 .
.
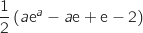 .
.
L'aire du quadrilatère OABB' est la somme des aires du triangle OAA' et du trapèze ABB'A' soit :
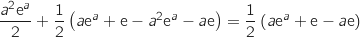 .
L'aire de la zone hachurée s'obtient en soustrayant à l'aire du quadrilatère OABB', l'aire de la zone délimitée par
.
L'aire de la zone hachurée s'obtient en soustrayant à l'aire du quadrilatère OABB', l'aire de la zone délimitée par  , l'axe des abscisses et les droites d'équations
, l'axe des abscisses et les droites d'équations 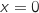 et
et  .
On remarque que pour tout
.
On remarque que pour tout 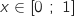 ,
, 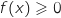 et donc que l'aire de la « zone sous la courbe » est égale à
et donc que l'aire de la « zone sous la courbe » est égale à 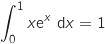 .
L'aire de la partie du plan hachurée vaut donc :
.
L'aire de la partie du plan hachurée vaut donc :
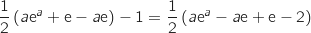 .
.
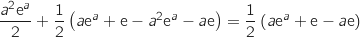 .
L'aire de la zone hachurée s'obtient en soustrayant à l'aire du quadrilatère OABB', l'aire de la zone délimitée par
.
L'aire de la zone hachurée s'obtient en soustrayant à l'aire du quadrilatère OABB', l'aire de la zone délimitée par  , l'axe des abscisses et les droites d'équations
, l'axe des abscisses et les droites d'équations 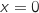 et
et  .
On remarque que pour tout
.
On remarque que pour tout 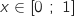 ,
, 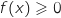 et donc que l'aire de la « zone sous la courbe » est égale à
et donc que l'aire de la « zone sous la courbe » est égale à 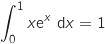 .
L'aire de la partie du plan hachurée vaut donc :
.
L'aire de la partie du plan hachurée vaut donc :
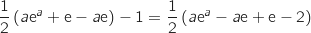 .
.
PARTIE B
Soit la fonction définie sur
la fonction définie sur 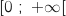 par
par
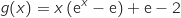
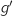 la fonction dérivée de la fonction
la fonction dérivée de la fonction  . Calculer
. Calculer 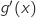 pour tout réel
pour tout réel  de
de 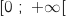 .
Vérifier que la fonction dérivée seconde
.
Vérifier que la fonction dérivée seconde 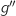 est d\'efinie sur
est d\'efinie sur 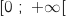 par
par 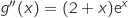 .
.
La fonction  est dérivable sur
est dérivable sur  et en utilisant la formule de la dérivée du produit on a :
et en utilisant la formule de la dérivée du produit on a :
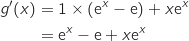 On dérive une seconde fois :
On dérive une seconde fois :
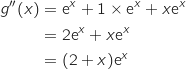
2. En déduire les variations de la fonction  est dérivable sur
est dérivable sur  et en utilisant la formule de la dérivée du produit on a :
et en utilisant la formule de la dérivée du produit on a :
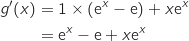 On dérive une seconde fois :
On dérive une seconde fois :
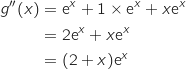
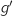 sur
sur 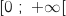 .
.
Pour tout 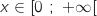 ,
, 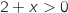 et donc
et donc 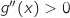 , donc
, donc 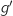 est croissante on a alors le tableau de variations :
est croissante on a alors le tableau de variations :
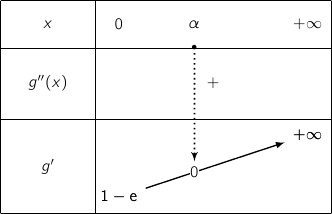
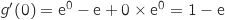 .
Limite en
.
Limite en  de
de 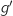
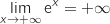 et par produit
et par produit 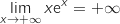 .
Finalement, par somme,
.
Finalement, par somme, 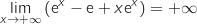 .
.
3. Etablir que l'équation 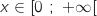 ,
, 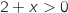 et donc
et donc 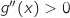 , donc
, donc 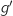 est croissante on a alors le tableau de variations :
est croissante on a alors le tableau de variations :

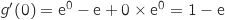 .
Limite en
.
Limite en  de
de 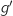
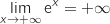 et par produit
et par produit 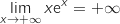 .
Finalement, par somme,
.
Finalement, par somme, 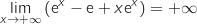 .
.
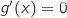 admet une solution unique
admet une solution unique  dans l'intervalle
dans l'intervalle 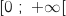 .
Déterminer une valeur approchée de
.
Déterminer une valeur approchée de  à
à 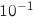 près.
près.
La fonction 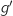 est définie, continue et strictement croissante sur
est définie, continue et strictement croissante sur  avec :
avec :
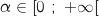 tel que
tel que 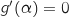 .
Avec la calculette on trouve
.
Avec la calculette on trouve 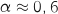 .
.
4. En déduire les variations de la fonction 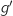 est définie, continue et strictement croissante sur
est définie, continue et strictement croissante sur  avec :
avec :
-
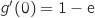 (négatif),
(négatif),
-
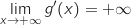
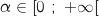 tel que
tel que 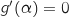 .
Avec la calculette on trouve
.
Avec la calculette on trouve 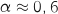 .
.
 sur
sur 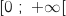 .
.
D'après ce qui précède on peut dresser le tableau de variations de  :
:
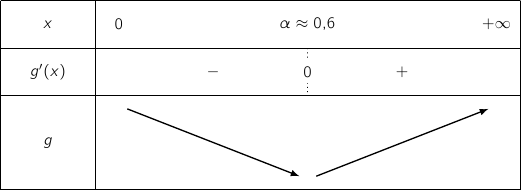
5. En utilisant les réponses aux questions des parties A et B, montrer qu'il existe une valeur de  :
:

 pour laquelle l'aire de la partie du plan hachurée est minimale. Donner cette valeur de
pour laquelle l'aire de la partie du plan hachurée est minimale. Donner cette valeur de  .
.
Pour tout 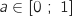 l'aire de la zone hachurée vaut :
l'aire de la zone hachurée vaut :
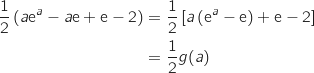 Or d'après l'étude précédente la fonction
Or d'après l'étude précédente la fonction  admet un minimum sur
admet un minimum sur  atteint en
atteint en  , donc l'aire de la partie hachurée est minimum pour
, donc l'aire de la partie hachurée est minimum pour 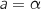 .
.
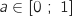 l'aire de la zone hachurée vaut :
l'aire de la zone hachurée vaut :
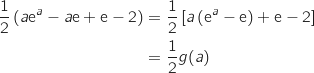 Or d'après l'étude précédente la fonction
Or d'après l'étude précédente la fonction  admet un minimum sur
admet un minimum sur  atteint en
atteint en  , donc l'aire de la partie hachurée est minimum pour
, donc l'aire de la partie hachurée est minimum pour 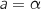 .
.
