Sujet et corrigé de l'exercice 2 du bac S de maths de mars 2014 en Nouvelle-Calédonie
Cacher les corrigés
Partie A
Restitution organisée de connaissances L'objectif de cette partie est de démontrer le théorème suivant : Si est une variable aléatoire suivant la loi normale centrée renduite, alors pour tout réel appartenant à l'intervalle , il existe un unique réel positif tel que . Soit la fonction définie et dérivable sur par :Soit la fonction définie et dérivable sur par :
1. Que représente la fonction pour la loi normale centrée réduite ?
C'est la fonction de densité.
2. Préciser et la limite de quand tend vers .
3. A l'aide de considérations graphiques montrer que pour tout réel positif , .
est positive sur et sa courbe est symétrique par rapport à l'axe des ordonnées.
Pour tout réel , les aires des domaines suivants sont identiques :
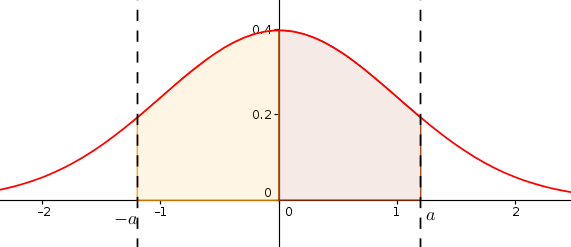
Donc
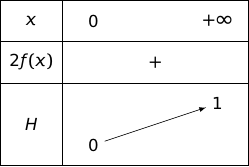
4. En déduire que la dérivée de la fonction sur est la fonction
et dresser le tableau de variations de sur .
- la courbe, l'axe des abscisses, les droites d'équations et ,
- la courbe, l'axe des abscisses, les droites d'équations et ,

Pour , la dérivée de est , donc .
La fonction est strictement positive sur , donc est strictement croissante.
5. Démontrer alors le théorème énoncé.

Le théorème équivaut à a un unique solution dans .
est continue et strictement croissante sur .
et
donc
D'après le théorème de la valeur intermédiaire a une unique solution dans , ce qui montre le théorème.
Partie B
Un laboratoire se fournit en pipettes auprès de deux entreprises, notées A et B. % des pipettes viennent de l'entreprise A et % des pipettes de cette entreprise possèdent un défaut. Dans le stock total du laboratoire, 5 % des pipettes présentent un défaut. On choisit au hasard une pipette dans le stock du laboratoire et on note :- A l'événement : « La pipette est fournie par l'entreprise A » ;
- B l'événement : « La pipette est fournie par l'entreprise B » ;
- D l'événement : « La pipette a un défaut ».
Un arbre pour voir plus clairement la situation :
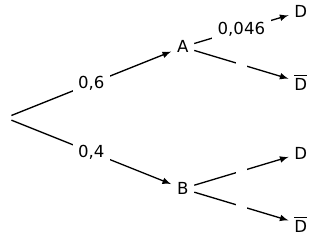
A et B partitionnent l'univers.
Formule des probabilités totales :
.
3. Parmi les pipettes venant de l'entreprise B, quel pourcentage de pipettes présente un défaut ?

soit %.
Partie C
Une pipette est dite conforme si sa contenance est comprise, au sens large entre 98 millilitres (mL) et 102 mL. Soit la variable aléatoire qui à chaque pipette prise au hasard dans le stock d'un laboratoire associe sa contenance (en millilitres). On admet que suit une loi normale de moyenne et écart type tels que et . 1. Quelle est alors la probabilité, à près, pour qu'une pipette prise au hasard soit conforme ? On pourra s'aider de la table ci-dessous ou utiliser une calculatrice.| Contenance (en mL) | 95 | 96 | 97 | 98 | 99 |
| (arrondi à ) | 0,000 00 | 0,000 04 | 0,001 65 | 0,025 06 | 0,163 68 |
| Contenance (en mL) | 100 | 101 | 102 | 103 | 104 |
| (arrondi à ) | 0,5 | 0,836 32 | 0,974 94 | 0,998 35 | 0,999 96 |
On peut vérifier ce résultat directement avec la calculette.
Pour la suite, on admet que la probabilité pour qu'une pipette soit non-conforme est .
2. On prélève dans le stock du laboratoire des échantillons de pipettes de taille , où
est un entier naturel supérieur ou égal à 100. On suppose que le stock est assez important pour considérer ces tirages comme indépendants.
Soit la variable aléatoire qui à chaque échantillon de taille associe le nombre de pipettes non-conformes de l'échantillon.
a. Quelle est la loi suivie par la variable aléatoire ?
suit la loi binomiale de paramètres et .
b. vérifier que , et .
On sait que , donc .
soit .
soit .
c. Donner en fonction de l'intervalle de fluctuation asymptotique au seuil de 95 % de la fréquence des pipettes non-conformes dans un échantillon.
soit
