Sujet et corrigé de l'exercice 3 du bac S de maths de mars 2014 en Nouvelle-Calédonie
Cacher les corrigés
Partie A
Soit la fonction dérivable, définie sur l'intervalle par :
1. Déterminer les limites de en 0 et en .
Limite à droite en 0
Limite connue vue en cours : .
Limite en
; ; par produit :
2. On appelle la fonction dérivée de sur . Montrer que
est dérivable sur et avec :
; et
;
Formule de la dérivée du produit : donc :
3. Déterminer les variations de sur .
Signe de la dérivée :
Pour tout :
soit
De même : et .
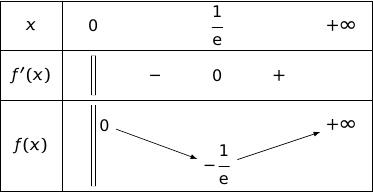
Tableau de variations
Partie B
Soit la courbe représentative de la fonction dans un repère orthonormal.
Soit l'aire, exprimée en unités d'aire, de la partie du plan comprise entre l'axe des abscisses, la courbe et les droites d'équations respectives et .
On utilise l'algorithme suivant pour calculer, par la méthode des rectangles, une valeur approchée de l'aire .

Algorithme :
Variables
et sont des nombres entiers
et sont des nombres réels.
Initialisation
prend la valeur 0
prend la valeur 0
prend la valeur 4
Traitement
Pour allant de 0 à
Affecter à la valeur
Affecter à la valeur
Fin pour
Affichage
Afficher
Afficher
1.a. Que représentent et sur le graphique précédent.
représente la somme des aires des rectangles quadrillés.
représente la somme des aires des rectangles simplement hachurés.
b. Quelles sont les valeurs et affichées en sortie de l'algorithme (on donnera une valeur approchée de par défaut à près et une valeur approchée par excès de à près) ?
c. En déduire un encadrement de .
2. Soient les suites et définies pour tout entier non nul par :
On admettra que, pour tout entier naturel non nul, .
a. Trouver le plus petit entier tel que .
Pour tout entier :
où .
Donc le plus petit entier tel que est 14.
b. Comment modifier l'algorithme précédent pour qu'il permette d'obtenir un encadrement de d'amplitude inférieure à 0,1 ?
Il suffit de remplacer dans l'initialisation l'instruction « prend la valeur 4 » par l'instruction « prend la valeur 14 ».
Partie C
Soit la fonction dérivable, définie sur par :
1. Montrer que est une primitive de sur .
Dérivée de en utilisant la formule de la dérivée du produit :
soit
Dérivée de :
soit
Donc
2. Calculer la valeur exacte de .
La fonction est continue et positive sur , donc :
