Sujet et corrigé de l'exercice 4 du bac S de maths de mars 2014 en Nouvelle-Calédonie
Cacher les corrigés
Soit ABCDEFGH un paralléllépipède rectangle tel que , et . On appelle respectivement I, J et P les milieux respectifs des segments [CD], [EF] et [AB]. On note Q le point défini par .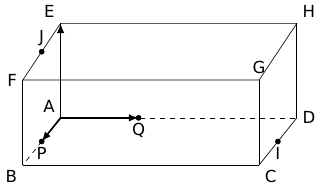
On appelle plan médiateur d'un segment le plan perpendiculaire à ce segment et passant par son milieu. L'objectif de l'exercice est de déterminer les coordonnées du centre d'une sphère circonscrite au tétraèdre ABIJ (c'est à dire une sphère qui passe par les quatre points A, B, I et J). L'espace est rapporté au repère orthonormal . 1. Justifier que les quatre points A, B, I et J ne sont pas coplanaires.
A, B et I ne sont pas alignés et ils définissent le plan de la face ABCD du paralléllépipède.
J est dans le plan de la face FGHE qui est strictement parallèle à (ABI), donc J n'appartient pas
à ce plan ce qui montre que A, B, I et J ne sont pas coplanaires.
2. Déterminer une équation cartésienne du plan médiateur du segment [AB].
Il passe par le milieu de [AB].
Un vecteur normal est
Une équation cartésienne est de la forme : soit
Il passe par P donc :
Une équation de est
3. Soit le plan d'équation cartésienne .
Montrer que le plan est le plan médiateur du segment [IJ].
et
Milieu de [IJ] : soit
, donc passe par le milieu de [IJ].
Vecteur normal de :
soit
Du coup , donc
est normal à , c'est à dire que est perpendiculaire à [IJ].
Ainsi est perpendiculaire à [IJ] et passe par son milieu donc c'est le plan médiateur du segment.
4.a. Démontrer que les plans et sont sécants.
Vecteur normal de :
Vecteur normal de :
Ces vecteurs ne sont pas colinéaires (pas de coefficient de proportionnalité pour passer des coordonnées de l'un à l'autre), donc les plans sont sécants.
b. Montrer que leur intersection est une droite dont une représentation paramétrique est :
où décrit l'ensemble des nombres réels .
L'intersection de deux plans est une droite.
On vérifie que les points de appartiennent aux deux plans :
: pour tout , , donc .
: pour tout , , donc .
La droite est incluse dans les deux plans sécants, donc est l'intersection des deux plans.
c. Déterminer les coordonnées du point de la droite tel que .
, donc et on cherche .
Donc
d. Montrer que le point est centre de la sphère circonscrite au tétraèdre ABIJ.
On sait déjà que
et
et
Du coup :
Cela prouve que est le centre de la sphère circonscrite à ABIJ.
