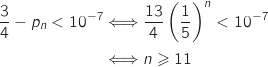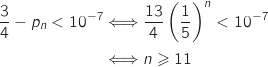Corrigé de l'exercice 2 de maths du bac S de juin 2011 en Polynésie
Cacher les corrigés
Un joueur débute un jeu vidéo et effectue plusieurs parties successives. On admet que :- la probabilité qu'il gagne la première partie est de 0,1
- s'il gagne une partie, la probabilité de gagner la suivante est égale à 0,8
- s'il perd une partie, la probabilité de gagner la suivante est égale à 0,6
non nul :
- G
l'évènement « le joueur gagne la -ième partie »
-
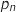la probabilité de l'évènement G
.
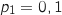1. Montrer que
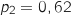. On pourra s'aider d'un arbre pondéré.
On a l'arbre de probabilités :
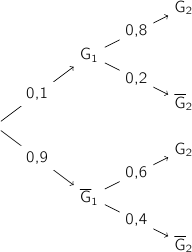
En utilisant la formule des probabilités totales on a :
.
.
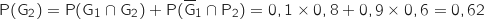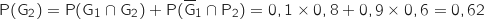2. Le joueur a gagné la deuxième partie. Calculer la probabilité qu'il ait perdu la première.
Il s'agit de calculer :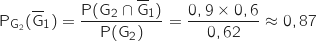 
.
3. Calculer la probabilité que le joueur gagne au moins une partie sur les trois premières parties.
.
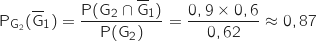On calcule d'abord la probabilité de l'événement contraire : le joueur ne gagne aucune partie soit :
.
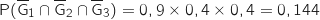Donc la probabilité de l'événement recherché est :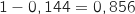 
.
4. Montrer que pour tout entier naturel .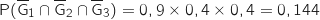
Donc la probabilité de l'événement recherché est : .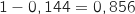
non nul,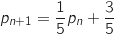 
.
On construit un arbre pour modéliser la situation entre la partie numéro et la partie numéro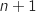 
:
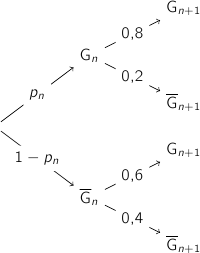
En utilisant la formule des probabilités totales on a :
.
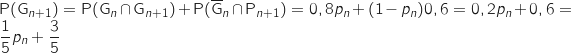5. Montrer par récurrence que, pour tout entier naturel et la partie numéro :
.
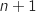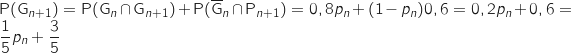non nul :
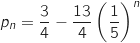
La propriété à montrer pour tout entier 
est :
«
».
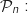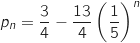Initialisation
Pour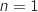 
, la formule donne : 
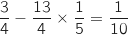ce qui correspond à 
.
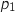Donc 
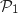est vraie.
Hérédité
On suppose que la propriété est vraie à un rang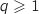 
, on a donc l'hypothèse de récurrence :
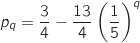On montre qu'alors la propriété est vraie au rang 
.
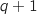D'après la question 4. on a :
Donc 
est vraie.
Ainsi la propriété est vraie au rang 1 et elle est héréditaire donc selon le principe de récurrence la propriété
est vraie pour tout entier .
6. Déterminer la limite de la suite est :
«
».
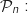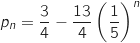Initialisation
Pour 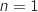, la formule donne : 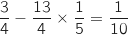ce qui correspond à .
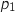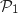Donc est vraie.
Hérédité
On suppose que la propriété est vraie à un rang 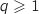, on a donc l'hypothèse de récurrence :
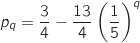On montre qu'alors la propriété est vraie au rang .
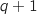D'après la question 4. on a :
Donc est vraie.
Ainsi la propriété est vraie au rang 1 et elle est héréditaire donc selon le principe de récurrence la propriété
est vraie pour tout entier .
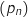quand tend vers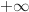 
.
Pour calculer cette limite on utilise la relation : .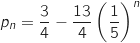
Comme 
, 
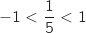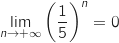et donc par produit et addition 
.
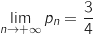7. Pour quelles valeurs de l'entier naturel .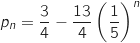
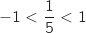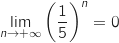Comme , et donc par produit et addition .
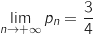a-t-on :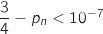 
?
On résout :
